题目内容
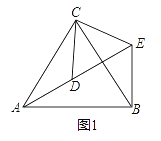
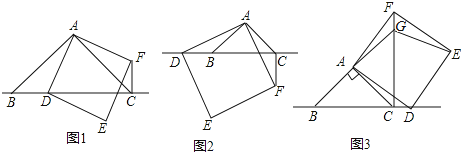
【题目】如图,正方形ABCD的边长为1,点E是BC边上一动点(点E不与点B、C重合),以线段DE为边长,作正方形DEFG,使得点F、G落在直线DE的下方,连接AF、BF.当△ABF为等腰三角形时,BE的长为_____.

【答案】![]() 或1-
或1-![]()
【解析】
分两种情形: ①如图1中, 当FA=FB时, 由ΔDCE≌ΔEMF, 推出FM=BM, 推出四边形BMNF是正方形即可解决问题.(2)如图2中,当BA=BF时,根据CE=BM=FN即可解决问题.
解: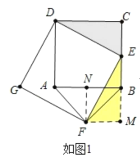
如图1中,当FA=FB时,作FN⊥AB于N,FM⊥CB于M,
![]() 四边形ABCD、DEFG是正方形,
四边形ABCD、DEFG是正方形,
![]() ∠C=∠DEF=∠M=∠ABC=
∠C=∠DEF=∠M=∠ABC=![]() ,DE=EF,DC=BC,
,DE=EF,DC=BC,
![]() ∠DEC+∠FEM=
∠DEC+∠FEM=![]() , ∠CDE+∠DEC=
, ∠CDE+∠DEC=![]() ,
,
![]() ∠CDE=∠FEM ,
∠CDE=∠FEM ,
在ΔDCE和ΔEMF中,
∠C=∠M,∠CDE=∠FEM ,DE=EF
![]() ΔDCE≌ΔEMF,
ΔDCE≌ΔEMF, ![]() FM=CE,CD=EM=BC
FM=CE,CD=EM=BC
![]() BM=EC=FM ,
BM=EC=FM ,
![]() ΔBMF是等腰直角三角形,
ΔBMF是等腰直角三角形,
![]() ∠FBM=∠FBN=
∠FBM=∠FBN=![]() ,
,
![]() ∠FNB=
∠FNB=![]() ,FA=FB,
,FA=FB,
![]() AN=BN=NF=
AN=BN=NF=![]()
![]() ∠M=∠MBN=∠BNF=
∠M=∠MBN=∠BNF=![]() ,
,![]() 四边形BMFN是矩形,
四边形BMFN是矩形,
![]() NF=NB,
NF=NB,
![]() 四边形BMFN 是正方形,
四边形BMFN 是正方形,
![]() BM=FN= CE=EB=
BM=FN= CE=EB=![]()
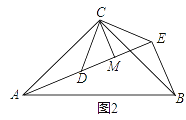
②如图2中, 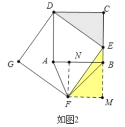
当BA=BF时,由(1)可知,ΔBNF是等腰直角三角形, BF=AB=1,
![]() BM=CE=FN=
BM=CE=FN=![]() ,
,
![]() EB=BC-CE=1-
EB=BC-CE=1-![]()
故答案为![]() 或1-
或1-![]() .
.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案【题目】某公司实行年工资制,职工的年工资由基础工资、住房补贴和医疗费三项组成,具体规定如下:
项目 | 第一年的工资(万元) | 一年后的计算方法 |
基础工资 | 1 | 每年的增长率相同 |
住房补贴 | 0.04 | 每年增加0.04 |
医疗费 | 0.1384 | 固定不变 |
(1)设基础工资每年增长率为x,用含x的代数式表示第三年的基础工资为 万元;
(2)某人在公司工作了3年,他算了一下这3年拿到的住房补贴和医疗费正好是这3年基础工资总额的18 %,问基础工资每年的增长率是多少?