��Ŀ����
����Ŀ������֪��ƽ���ı����кܶ����ʣ�����������ǰ�ƽ���ı�����������һ���Խ��߷��ۣ��ᷢ�������л��и���Ľ��ۣ�
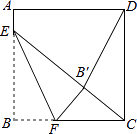
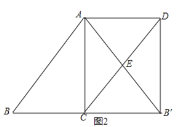
��������֤������![]() ABCD�У�AB��BC������ABC��AC��������AB��C������B��D��
ABCD��AB��BC������ABC��AC��������AB��C������B��D��
��1����գ�B��E DE���<������>������
��2����֤��B��D��AC��
��Ӧ����̽����
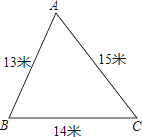
(3)��![]() ABCD�У���֪��BC=4����B=60�㣬����ABC��AC��������AB��C������B��D������A��C��D��B��Ϊ������ı����Ǿ��Σ���AC�ij���
ABCD�У���֪��BC=4����B=60�㣬����ABC��AC��������AB��C������B��D������A��C��D��B��Ϊ������ı����Ǿ��Σ���AC�ij���
���𰸡���1��=����2������������3��2![]() ��4
��4![]() .
.
��������
(1)��ƽ���ı��ε����ʵó���EAC=��ACB���ɷ��۵����ʵó���ACB=��ACB�䣬֤����EAC=��ACB'���ó�AE=CE���Ӷ�DE=B'E
(2)���ݵ��������ε����ʵó�DE=B'E��֤����B��DA=![]() (180��B��ED)���ɡ�AEC=��B'ED���ó���ACB'=��CB'D�����ɵó�B'D//AC��
(180��B��ED)���ɡ�AEC=��B'ED���ó���ACB'=��CB'D�����ɵó�B'D//AC��
(3)��������������ɾ��ε����ʵó���CAB'=90�㣬�ó���BAC=90�㣬����30��ֱ�����������ʼ������AC=2![]() �����ɾ��ε����ʺ���֪�����ó�AC=4
�����ɾ��ε����ʺ���֪�����ó�AC=4![]() ��
��
��1���⣺���ı���ABCD��ƽ���ı��Σ�
��AD=BC��AD//BC��
���EAC=��ACB��
�ߡ�ABC�ա�AB'C��
���ACB=��ACB'��BC=B'C��
���EAC=��ACB'��
��AE=CE��
��DE=B��E��
�ʴ�Ϊ=.
��2��֤������DE=B'E
���C B'D=��B��DA=![]() (180-��B'ED)
(180-��B'ED)
�ߡ�AEC=��B'ED
���AC B'=��C B'D
��B'D��AC
��3���⣺���һ����ͼ1
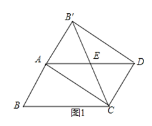
���ı���ACDB���Ǿ��Σ�
���CAB��=90�㣬
���BAC=90��
�ߡ�B=60��
��AC=![]() BC=2
BC=2![]()
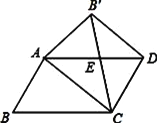
���������ͼ2
���ı���ACB��D�Ǿ��Σ�
���ACB��=90��
���ACB=90��
��BC=4����B=60��
��AC=4![]() ��
��
����������ACAC�ij�Ϊ2![]() ��4
��4![]() ��
��

����Ŀ��ijУ��ѧ��ȤС���ԱС���Ա�����ѧ����ĩ������ѧ�ɼ����ɼ�ȡ����������Ϊ100�֣�����ͳ�Ʒ��������Ƴ�����Ƶ���ֲ�ֱ��ͼ��Ƶ����Ƶ�ʷֲ������������ͼ���ṩ����Ϣ������������⣺
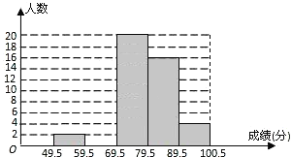
���� | 49.5��59.5 | 59.5��69.5 | 69.5��79.5 | 79.5��89.5 | 89.5��100.5 | �ϼ� |
Ƶ�� | 2 |
| 20 | 16 | 4 | 50 |
Ƶ�� | 0.04 | 0.16 | 0.40 | 0.32 |
| 1 |
��1��Ƶ����Ƶ�ʷֲ�����![]() ��
��![]() ��
��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����ѧ��ʦ���Ӳ�����90�ֵ�ѧ����ѡ1�˽���ѧϰ���飬��ôȡ����93�ֵ�С����ѡ�ϵĸ����Ƕ��٣�