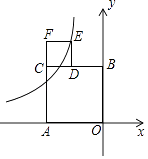题目内容
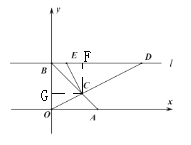
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,过点
,过点![]() 画
画![]() 轴的垂线
轴的垂线![]() ,点
,点![]() 在线段
在线段![]() 上,连结
上,连结![]() 并延长交直线
并延长交直线![]() 于点
于点![]() ,过点
,过点![]() 画
画![]() 交直线
交直线![]() 于点
于点![]() .
.
(1)求![]() 的度数,并直接写出直线
的度数,并直接写出直线![]() 的解析式;
的解析式;
(2)若点![]() 的横坐标为2,求
的横坐标为2,求![]() 的长;
的长;
(3)当![]() 时,求点
时,求点![]() 的坐标.
的坐标.

【答案】(1)![]() ;(2)1;(3)C的坐标为(2,1)或(1,2)
;(2)1;(3)C的坐标为(2,1)或(1,2)
【解析】
(1)根据A(3,0),B(0,3),得到OA=OB=3,则![]() 是等腰直角三角形,即可求出
是等腰直角三角形,即可求出![]() 的度数,根据待定系数法即可求出直线
的度数,根据待定系数法即可求出直线![]() 的解析式;
的解析式;
(2)作CF⊥l于F,CG⊥y轴于G,根据点C的横坐标为2,点C在![]() 上,求出点C(2,1),CG=BF=2,OG=1,证明Rt△OGC≌Rt△EFC,即可求解.
上,求出点C(2,1),CG=BF=2,OG=1,证明Rt△OGC≌Rt△EFC,即可求解.
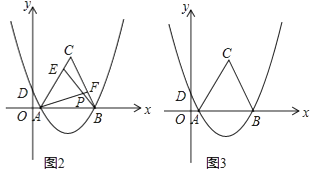
(3)分E在点B的右侧和E在点B的左侧两种情况进行讨论即可.
(1)∵A(3,0),B(0,3)
∴OA=OB=3
∵∠AOB=90°
∴∠OBA=45°
直线AB的解析式为:![]()
(2)作CF⊥l于F,CG⊥y轴于G
∴∠OGC=∠EFC=90°
∵点C的横坐标为2,点C在![]() 上
上
∴C(2,1),CG=BF=2,OG=1
∵BC平分∠OBE
∴CF=CG =2
∵∠OCE=∠GCF=90°
∴∠OCG=∠ECF
∴Rt△OGC≌Rt△EFC(ASA)
∴EF=OG =1
∴BE =1
(3)设C的坐标为(m,-m+3)
当E在点B的右侧时,由(2)知EF=OG =m-1
∴m-1=-m+3
∴m=2
∴C的坐标为(2,1)
当E在点B的左侧时, 同理可得:m+1=-m+3
∴m=1
∴C的坐标为(1,2)

 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案【题目】近几年,全社会对空气污染问题越来越重视,空气净化器的销量也在逐年增加.某商场从厂家购进了A、B两种型号的空气净化器,两种净化器的销售相关信息见下表:
A型销售数量(台) | B型销售数量(台) | 总利润(元) |
5 | 10 | 2000 |
10 | 5 | 2500 |
(1)每台A型空气净化器和B型空气净化器的销售利润分别是多少?
(2)该公司计划一次购进两种型号的空气净化器共100台,其中B型空气净化器的进货量不少于A型空气净化器的2倍,为使该公司销售完这100台空气净化器后的总利润最大,请你设计相应的进货方案;
(3)已知A型空气净化器的净化能力为300m3/小时,B型空气净化器的净化能力为200m3/小时,某长方体室内活动场地的总面积为200m2 , 室内墙高3m,该场地负责人计划购买5台空气净化器每天花费30分钟将室内就欧诺个气净化一新,若不考虑空气对流等因素,至少要购买A型空气净化器多少台?