Question

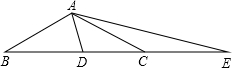
如图，在△ABC中，∠BAC=120°，AB=AC，点D在BC上，且BD=BA，点E在BC的延长线上，且CE=CA．
（1）试求∠DAE的度数．
（2）如果把题中“AB=AC”的条件去掉，其余条件不变，那么∠DAE的度数会改变吗？
（3）若∠BAC=α°，其它条件与（2）相同，则∠DAE的度数是多少？

Answer 1

（1）因为AB=AC，
所以∠B=∠ACB=30°，
因为BA=BD，所以，∠BAD=∠BDA=75°，
所以∠DAC=45°，
又有CA=CE，
所以∠E=∠CAE=15°，
所以∠DAE=∠DAC+∠CAE=60°；

（2）不改变；令∠B=x°，BA=BD，
所以∠BAD=∠BDA=

180°-∠B

2

=90°-

1

2

x°，
∠ACB=180°-∠ACE=∠B+∠BAC，得∠ACB=60°-x°，
所以∠DAC=∠ADB-∠ACD=30°+

1

2

x°，
又因为CA=CE，
所以∠E=∠CAE=30°-

1

2

x°，
所以∠DAE=∠DAC+∠CAE=60°

（3）

1

2

α°．
设∠B=x°，
∵BA=BD，
所以∠BAD=∠BDA=90°-

1

2

x°，∠ACB=180°-x°-α°，
所以∠DAC=∠ADB-∠ACD=-90°+

1

2

x°+α°，
又因为CA=CE，
所以∠E=∠CAE=90°-

1

2

x°-

1

2

α°，
所以∠DAE=∠DAC+∠CAE=

1

2

α°