题目内容
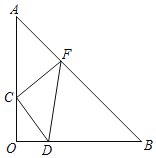
【题目】如图,E,F是正方形ABCD外接圆上的两个点,且EC∥BF,AD与BF的延长线交于点P.
(1)求∠EBF的度数;
(2)求证:BPBE=![]() AB2.
AB2.
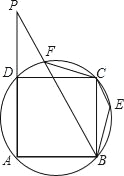
【答案】(1)45°(2)证明见解析
【解析】
(1)根据已知条件得到弧CAB的度数=270°,由圆周角定理得到![]() 根据平行线的性质证得∠E+∠EBF=180°,可得到∠EBF=45°;
根据平行线的性质证得∠E+∠EBF=180°,可得到∠EBF=45°;
(2)连接BD,根据正方形的性质得到∠ADB=45°,![]() ,AP∥BC,AB=BC,根据邻补角的定义得到∠PDB=135°,根据平行线的性质得到∠P=∠PBC=∠ECB,推出△PBD∽△BCE,根据相似三角形的性质得到
,AP∥BC,AB=BC,根据邻补角的定义得到∠PDB=135°,根据平行线的性质得到∠P=∠PBC=∠ECB,推出△PBD∽△BCE,根据相似三角形的性质得到![]() 等量代换即可得到结论.
等量代换即可得到结论.
(1)∵四边形ABCD是正方形,
∴弧CAB的度数=270°,
∴![]()
∵EC∥BP,
∴∠E+∠EBF=180°,
∴∠EBF=45°;
(2)连接BD,
∵四边形ABCD是正方形,
∴∠ADB=45°,![]() ,AP∥BC,AB=BC,
,AP∥BC,AB=BC,
∴∠PDB=135°,
∴∠PDB=∠E,
∵AP∥BC,CE∥PB,
∴∠P=∠PBC=∠ECB,
∴△PBD∽△BCE,
∴![]()
∴![]()
∴![]()

练习册系列答案
相关题目
【题目】甲、乙两名队员参加设计训练,成绩分别被制成下列两个统计图:
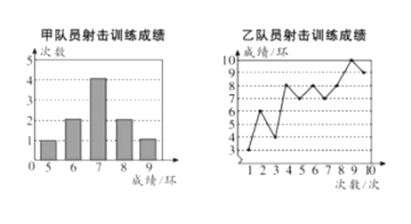
根据以上信息,整理分析数据如下:
平均数(环) | 中位数(环) | 众数(环) | 方差 | |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)表格中![]() ,
,![]() ,
,![]() ;
;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩,若选派其中一名参赛,你认为应选哪名队员?
(3)如果乙再射击![]() 次,命中
次,命中![]() 环,那么乙的射击成绩的方差 .(填“变大”“变小”或“不变”)
环,那么乙的射击成绩的方差 .(填“变大”“变小”或“不变”)