题目内容
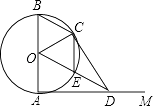
【题目】如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE. 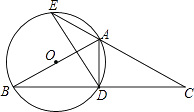
(1)求证:D是BC的中点;
(2)若DE=3,BD﹣AD=2,求⊙O的半径;
(3)在(2)的条件下,求弦AE的长.
【答案】
(1)证明:∵AB是圆O的直径,
∴AD⊥BC,
∵AB=AC,
∴BD=DC
(2)解:∵AB=AC,
∠B=∠C,
∵∠B=∠E,
∴∠E=∠C,
∴BD=DC=DE=3,
∵BD﹣AD=2,
∴AD=1,
在RT△ABD中,AB= ![]() =
= ![]() ,
,
∴⊙O的半径为 ![]()
(3)解:∵AB=AC= ![]() ,BD=DC=3,
,BD=DC=3,
∴BC=6,
∵∠B=∠E,∠C=∠C,
∴△EDC∽△BAC,
∵ACEC=DCBC,
∴ ![]() EC=3×6,
EC=3×6,
∴EC= ![]() ,
,
∴AE=EC﹣AC= ![]() ﹣
﹣ ![]() =
= ![]()
【解析】(1)根据圆周角定理求得AD⊥BC,根据等腰三角形三线合一的性质即可证得结论;(2)先求得∠E=∠C,根据等角对等边求得BD=DC=DE=3,进而求得AD=1,然后根据勾股定理求得AB,即可求得圆的半径;(3)根据题意得到AC= ![]() ,BC=6,DC=3,然后根据割线定理即可求得EC,进而求得AE.
,BC=6,DC=3,然后根据割线定理即可求得EC,进而求得AE.
【考点精析】掌握等腰三角形的性质和圆周角定理是解答本题的根本,需要知道等腰三角形的两个底角相等(简称:等边对等角);顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案【题目】中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3 000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
成绩x/分 | 频数/人 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |

根据所给信息,解答下列问题:
(1)m=_________,n=_________;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在_________分数段;