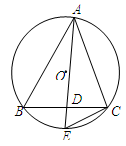
题目内容
如图,在□ABCD中,点P为边AB上的一点,E,F分别是PD,PC的中点,CD=2.则①EF= ;②设△PEF,△PAD,△PBC的面积分别为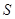 、
、 、
、 .已知
.已知 ,则
,则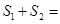 .
.

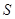 、
、 、
、 .已知
.已知 ,则
,则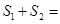 .
.
1, 12.
试题分析:①∵E,F分别是PD,PC的中点,CD=2
∴EF=
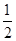 CD=1
CD=1②过P作PQ∥BC交DC于点Q,由BC∥AD,得到PQ∥AD,

∴四边形PQCB与四边形APQD都为平行四边形,
∴△PDA≌△DQP,△CBP≌△PQC,
∴S△PDA=S△DQP,S△CBP=S△PQC,
∵EF为△PCD的中位线,
∴EF∥DC,EF=
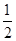 CD,
CD,∴△PEF∽△PCD,且相似比为1:2,
∴S△PEF:S△PCD=1:4,S△PEF=3,
∴S△PDC=S△DQP+S△QPC=S△PAD+S△PBC=S1+S2=12.
故答案是1,12.

练习册系列答案
相关题目
 ,则CD的长为_________________.
,则CD的长为_________________.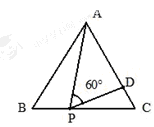

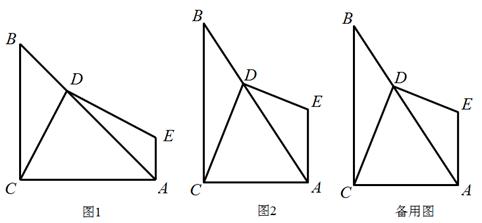
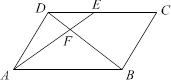
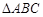 中,
中, ,
,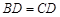 ,
, 于
于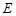 .求证:
.求证: .
. 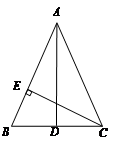
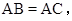
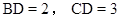 ,
,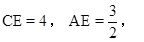 ,∠FDE=∠B,那么AF的长为( )
,∠FDE=∠B,那么AF的长为( )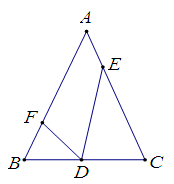
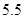 B.
B.  C.
C. 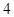 D.
D.