题目内容
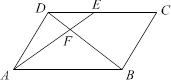
如图,在平行四边形ABCD中,E为CD上一点,连结AE,BD,且AE,BD交于点F,S△DEF∶S△ABF=4∶25,求DE∶EC的值.

2:3.
试题分析:先根据平行四边形的性质及相似三角形的判定定理得出△DEF∽△BAF,再根据S△DEF:S△ABF=4:10:25即可得出其相似比,由相似三角形的性质即可求出DE:AB 的值,由AB=CD即可得出结论.
试题解析:
∵四边形ABCD是平行四边形,
∴AB∥CD.
∴△DEF∽△BAF.
∴
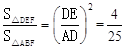 .
.∴
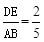 .
.又∵AB=CD,
∴DE∶EC=2∶3.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 ,那么
,那么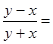 .
.
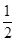 ∠BAF,AF=
∠BAF,AF=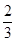 AD,试探究线段FM和FN之间的数量关系,并证明你的结论.
AD,试探究线段FM和FN之间的数量关系,并证明你的结论.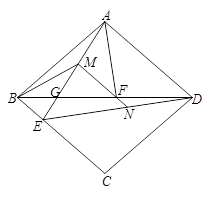
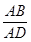 = .
= .
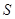 、
、 、
、 .已知
.已知 ,则
,则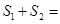 .
.



 ,则△EFC的周长为( )
,则△EFC的周长为( )