题目内容
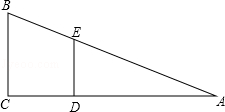
如图,等边三角形ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60 ,则CD的长为_________________.
,则CD的长为_________________.
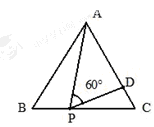
 ,则CD的长为_________________.
,则CD的长为_________________.
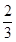 .
.试题分析:根据相似三角形的判定定理求出△ABP∽△PCD,再根据相似三角形对应边的比等于相似比的平方解答.
试题解析:∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵∠APB=∠PAC+∠C,∠PDC=∠PAC+∠APD,
∵∠APD=60°,
∴∠APB=∠PAC+60°,∠PDC=∠PAC+60°,
∴∠APB=∠PDC,
又∵∠B=∠C=60°,
∴△ABP∽△PCD,
∴
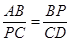 ,
,即
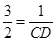 ,
,∴CD=
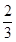 .
.考点: 1.相似三角形的判定与性质;2.等边三角形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
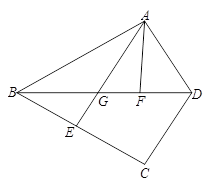
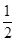 ∠BAF,AF=
∠BAF,AF=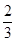 AD,试探究线段FM和FN之间的数量关系,并证明你的结论.
AD,试探究线段FM和FN之间的数量关系,并证明你的结论.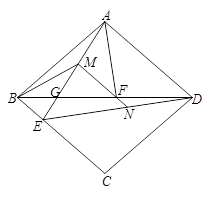
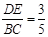 ,那么
,那么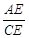 的值等于 .
的值等于 .
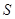 、
、 、
、 .已知
.已知 ,则
,则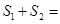 .
.
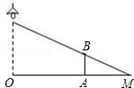
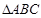 相似的是( )
相似的是( )