题目内容
函数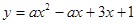 的图象与x轴有且只有一个交点,写出a所有可能的值____.
的图象与x轴有且只有一个交点,写出a所有可能的值____.
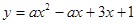 的图象与x轴有且只有一个交点,写出a所有可能的值____.
的图象与x轴有且只有一个交点,写出a所有可能的值____.0、1、9
试题分析:当
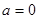 时,
时,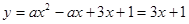 为一次函数,图象与x轴有且只有一个交点;当
为一次函数,图象与x轴有且只有一个交点;当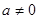 时,
时,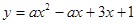 为二次函数,当
为二次函数,当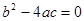 时,图象与x轴有且只有一个交点.
时,图象与x轴有且只有一个交点.当
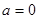 时,
时,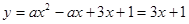 为一次函数,图象与x轴有且只有一个交点;
为一次函数,图象与x轴有且只有一个交点;当
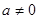 时,
时,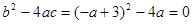 ,解得
,解得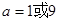
则a=0、1、9.
点评:二次函数
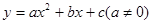 :当图象与x轴有两个交点时,
:当图象与x轴有两个交点时,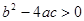 ;当图象与x轴只有一个交点时,
;当图象与x轴只有一个交点时,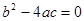 ;当图象与x轴没有交点时,
;当图象与x轴没有交点时,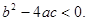

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
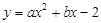 经过(2,1)和(6,-5)两点.
经过(2,1)和(6,-5)两点.
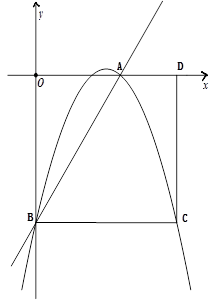
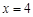 右侧的此抛物线上一点,过点P作PM
右侧的此抛物线上一点,过点P作PM
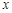 轴,垂足为M. 若以A、P、M为顶点的三角形与△OCB相似,求点P的坐标;
轴,垂足为M. 若以A、P、M为顶点的三角形与△OCB相似,求点P的坐标; 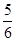 .
.
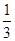 x2+bx+c经过点A、B,请求出这条抛物线的解析式;
x2+bx+c经过点A、B,请求出这条抛物线的解析式;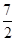 ≤x≤7,在抛物线上存在点P,使△ABP的面积最大,那么△ABP最大面积是 .(请直接写出结论,不需要写过程)
≤x≤7,在抛物线上存在点P,使△ABP的面积最大,那么△ABP最大面积是 .(请直接写出结论,不需要写过程)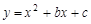 与
与 轴交于点
轴交于点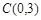 ,与
,与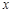 轴交于
轴交于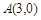 ,B两点(点A在点B的右侧),过C作直线
,B两点(点A在点B的右侧),过C作直线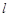 ,与抛物线相交于点
,与抛物线相交于点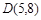 ,与对称轴交于点N,点
,与对称轴交于点N,点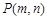 为直线
为直线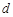
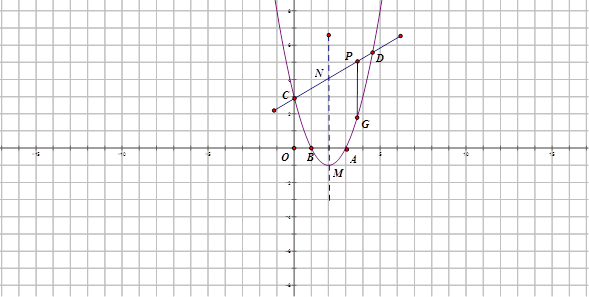
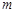 <5时,请用含
<5时,请用含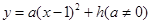 与
与 轴交于A(
轴交于A(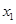 ,0)、B(3,0)两点,则
,0)、B(3,0)两点,则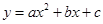 的图象如图所示,则一次函数
的图象如图所示,则一次函数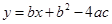 与反比例函数
与反比例函数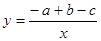 在同一坐标系内的图象可能为 ( )
在同一坐标系内的图象可能为 ( )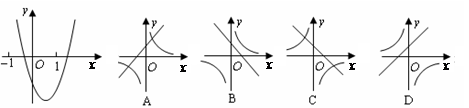
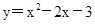 ,当
,当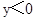 时自变量x的取值范围是 。
时自变量x的取值范围是 。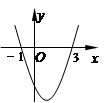
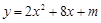 与x轴只有一个公共点,则m的值为 .
与x轴只有一个公共点,则m的值为 .