Question

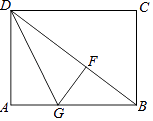
【题目】如图，四边形ABCD是矩形，DG平分∠ADB交AB于点G，GF⊥BD于F．
（1）求证：△ADG≌△FDG；
（2）若BG=2AG，BD=2 ，求AD的长．

Answer 1

【答案】
（1）证明：∵四边形ABCD是矩形，GF⊥BD，

∴∠A=∠DFG=90°，又∠ADG=∠FDG，DG=DG，

在△ADG和△FGD中，

，

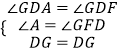∴△ADG≌△FDG．

（2）解：由（1）得△ADG≌△FDG，

∴FG=AG，

∵BG=2AG，

∴BG=2FG，

∴在Rt△BFG中，sin∠FBG= ，

∴∠FBG=30°，

∴AD= ．

【解析】（1）根据AAS即可证明△ADG≌△FDG；（2）只要证明∠FBG=30°，即可推出AD= BD，由此即可解决问题；