��Ŀ����
����Ŀ�����壺��ͼ1����ƽ��ֱ������ϵ�У���![]() �Ƕ��κ���
�Ƕ��κ���![]() ͼ����һ�㣬����
ͼ����һ�㣬����![]() ��
��![]() �ᣬ������κ���
�ᣬ������κ���![]() ��ͼ����
��ͼ����![]() ����
����![]() ����Գƣ����
����Գƣ����![]() ��
��![]() ���ڵ�
���ڵ�![]() �İ��溯������ͼ2����ƽ��ֱ������ϵ�У����κ���
�İ��溯������ͼ2����ƽ��ֱ������ϵ�У����κ���![]() �ĺ�������ʽ��
�ĺ�������ʽ��![]() ����
����![]() �Ƕ��κ���
�Ƕ��κ���![]() ͼ����һ�㣬�ҵ�
ͼ����һ�㣬�ҵ�![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() �����κ���
�������![]() ��
��![]() ���ڵ�
���ڵ�![]() �İ��溯����
�İ��溯����
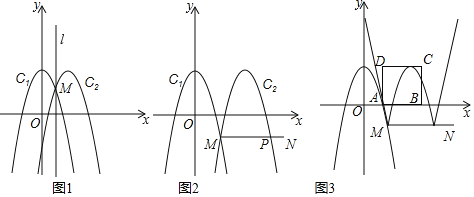
��1����![]() ����
����![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2������![]() ��
��![]() �ᣬ���
�ᣬ���![]() ���߶�
���߶�![]() ��
��![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() ����
����![]() ����
����![]() ��ֵ��
��ֵ��
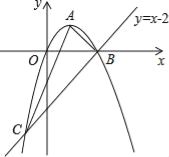
��3����ͼ3�����κ���![]() ��ͼ����
��ͼ����![]() �Ϸ��IJ��ּ�Ϊ
�Ϸ��IJ��ּ�Ϊ![]() ��ʣ��IJ�����
��ʣ��IJ�����![]() ���۵õ�
���۵õ�![]() ����
����![]() ��
��![]() ����ɵ�ͼ���Ϊ
����ɵ�ͼ���Ϊ![]() ����
����![]() ��
��![]() ������
Ϊ������![]() ���Ϸ���������
���Ϸ���������![]() ��ֱ��д��������
��ֱ��д��������![]() ��
��![]() ������������ʱ
������������ʱ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡�(1)![]() ;(2)
;(2) ![]() ;(3)������.
;(3)������.
��������
��1����![]() ʱ��������
ʱ��������![]() ��������
��������![]() ����ֱ��
����ֱ��![]() �Գƣ��ó�������
�Գƣ��ó�������![]() �Ķ���ʱ
�Ķ���ʱ![]() ���������
���������![]() �Ľ���ʽ����2����
�Ľ���ʽ����2����![]() �ᣬ
�ᣬ![]() ����
����![]() ���ٷ�
���ٷ�![]() ��
��![]() �������ۼ���;��3������ͼ���֪����
�������ۼ���;��3������ͼ���֪����![]() ʱ����֪
ʱ����֪![]() ��
��![]() �ĶԳ������ֱ��
�ĶԳ������ֱ��![]() �Գƣ�
�Գƣ�![]() �Ķ���ǡ��
�Ķ���ǡ��![]() �ϣ���ʱ
�ϣ���ʱ![]() ��������ǡ��2�����㣬�ʿɵó�����.
��������ǡ��2�����㣬�ʿɵó�����.
�⣺��1����![]() ʱ��������
ʱ��������![]() ��������
��������![]() ����ֱ��
����ֱ��![]() �Գƣ�
�Գƣ�
��������![]() �Ķ���ʱ
�Ķ���ʱ![]() ��
��
��������![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() .
.
��2����![]() �ᣬ
�ᣬ![]() ��
��
��![]() .
.
��![]() ʱ��
ʱ��![]() ��
��
![]() .
.
��![]() ʱ��
ʱ��![]() ��
��
![]() .
.
��3������ͼ���֪����![]() ʱ����֪
ʱ����֪![]() ��
��![]() �ĶԳ������ֱ��
�ĶԳ������ֱ��![]() �Գƣ�
�Գƣ�![]() �Ķ���ǡ��
�Ķ���ǡ��![]() �ϣ���ʱ
�ϣ���ʱ![]() ��������ǡ��2�����㣮
��������ǡ��2�����㣮
��![]() ʱ��ֱ��
ʱ��ֱ��![]() ��
��![]() ���غϣ�
���غϣ�![]() ��������ǡ���������㣮
��������ǡ���������㣮
��![]() ʱ��
ʱ��![]() ����
����![]() ��
��![]() �Գ�����ಿ��������������������
�Գ�����ಿ��������������������
��![]() ��
��![]() ʱ��
ʱ��![]() ��������
��������![]() �����������㣮
�����������㣮