Question

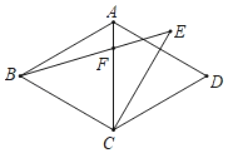
【题目】如图，在□ABCD中，E是AD的中点，BE交AC于点F，若△AEF的面积为3，则四边形EFCD的面积是_________

Answer 1

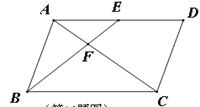
【答案】15

【解析】

由四边形ABCD是平行四边形，可证得△AEF∽△CBF，又由点E是AD中点，△AEF的面积为3，即可求得△EFC，△EDC的面积，即可求得答案．

解：连接EC，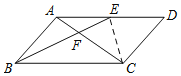

∵E是AD的中点，
∴AE=ED=AD，
∵四边形ABCD是平行四边形，
∴AD=BC，AD∥BC，
∴△AEF∽△CBF，
∴，
∴，
∵△AEF的面积为3，
∴S△EFC=2S△AEF=6，
∴S△AEC=9，
∵AE=ED，
∴S△AEC=S△EDC=9，
∴四边形EFCD的面积=S△ACD-S△AEF=18-3=15.
故答案为：15．