题目内容
二次函数
的图象如图所示，则m的值是
| A．－8 | B．8 | C．±8 | D．6 |
B
解析试题分析：根据抛物线与x轴只有一个交点，对应的一元二次方程根的判别式△=0（或由抛物线顶点的纵坐标等于0），列式求出m的值，再根据对称轴在y轴的左边求出m的取值范围，从而得解：
∵由图可知，抛物线与x轴只有一个交点，
∴对应的一元二次方程
的△=m2﹣4×2×8=0，解得m=±8，
∵对称轴为直线
，∴m＞0。
∴m的值为8。故选B。
练习册系列答案
挑战100单元检测试卷系列答案
名题金卷系列答案
相关题目
函数y=x2+bx+c与y=x的图象如图所示，有以下结论：①b2﹣4c＞0；②b+c+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．其中正确的个数为（ ）
| A．1 | B．2 | C．3 | D．4 |
如图所示，抛物线顶点坐标是P（1，3），则函数y随自变量x的增大而减小的x的取值范围是（ ）
| A．x>3 | B．x<3 | C．x>1 | D．x<1 |
二次函数
的图象如图所示，有下列结论：
①
，②
，③
，④ 
，⑤
其中正确的个数有（ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
若二次函数y=ax2+bx+c的x与y的部分对应值如下表：则下列说法错误的是( )
| A．二次函数图像与x轴交点有两个 |
| B．x≥2时y随x的增大而增大 |
| C．二次函数图像与x轴交点横坐标一个在－1~0之间，另一个在2~3之间 |
| D．对称轴为直线x=1.5 |
如图，已知抛物线
的对称轴为
，点A，B均在抛物线上，且
与x轴平行，其中点
的坐标为（n，3），则点
的坐标为( )．
| A．（n+2，3） | B．（ ，3） | C．（ ，3） | D．（ ，3） |
二次函数
的图象的顶点坐标是【 】
| A．（1，3） | B．（ ，3） | C．（1， ） | D．（，） |
在二次函数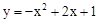
的图像中，若
随
的增大而增大，则的取值范围是
A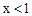． | B． | C． | D． |