题目内容
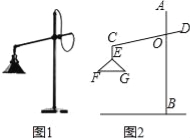
【题目】如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.
(1)求∠CEG的度数.
(2)求灯罩的宽度(FG的长;结果精确到0.1cm,可用科学计算器).
(参考数据:sin40°≈0.643,cos40°≈0.766,sin70°≈0.940,cos70°≈0.342)
【答案】(1)130°;(2)13.6cm.
【解析】
试题分析:(1)由EF=EG可知∠G=∠F=40°,由三角形的内角和为180°可求出∠FEG的大小,根据已知条件可得知∠CEF=∠CEG,由∠CEF+∠FEG+∠GEC为周角可得出结论;(2)延长FG交AB于点N,过点C作CM⊥AB于点M,延长CE交FG于点H,可知四边形CHNM为长方形,在Rt△CMO中由三角函数值求出CM的长度,再结合点G到OB的距离为12cm可求出HG的长度,由△EFG为等腰三角形可得知FG=2HG,从而得出结论.
试题解析:(1)如上图2:∵EF=EG,∠F=40°,∴∠G=40°,∠FEG=180°﹣∠F﹣∠G=100°,∵灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,∴∠CEG=∠CEF=![]() =
=![]() =130°;(2)如图所示.延长FG交AB于点N,过点C作CM⊥AB于点M,延长CE交FG于点H,
=130°;(2)如图所示.延长FG交AB于点N,过点C作CM⊥AB于点M,延长CE交FG于点H,
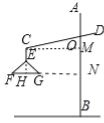
∵CE∥AB,FG处于水平位置,CM⊥AB,∴四边形CHNM为长方形,CH⊥FG,∴CM=HN.在Rt△OMC中,OC=20cm,∠COM=70°,∠OMC=90°,∴CM=OCsin∠COM≈20×0.940=18.8(cm),∵GN=12cm,HN=CM,∴HG=CM﹣GN=6.8(cm).∵EF=EG,CH⊥FG,∴FH=HG=![]() FG,∴FG=2×6.8=13.6(cm).所以灯罩的宽度为13.6cm.
FG,∴FG=2×6.8=13.6(cm).所以灯罩的宽度为13.6cm.

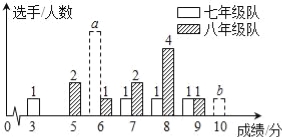
【题目】2015年10月29日,党的十八届五种全会胜利闭幕,某中学七、八年级各选派10名选手参加“党的十八届五中全会知识竞赛”计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
队别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
七年级 | 6.7 | m | 3.41 | 90% | n |
八年级 | 7.1 | 7.5 | 1.69 | 80% | 10% |
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m= ,n= ;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
【题目】在一次实验中,小明把一根弹簧的上端固定,在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体的质量x的一组对应值:
所挂重量x(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧长度y(cm) | 18 | 20 | 22 | 24 | 26 | 28 |
(1)上述反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)写出y与x之间的关系式,并求出当所挂重物为6kg时,弹簧的长度为多少?