Question

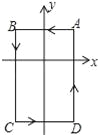
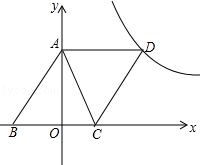
【题目】如图，点A（1，3）、点B（m，1）是一次函数的图像上的两点，一次函数图像与x轴交于点D.

（1）b = ，m = ；

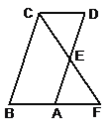
（2）过点B作直线l垂直于x轴，点E是点D关于直线l的对称点，点C是点A关于原点的对称点．试判断点B、E、C是否在同一条直线上，并说明理由．

（3）连结AO、BO，求△AOB的面积；

Answer 1

【答案】（1）b=4,m=3;（2）详见解析；（3）4.

【解析】试题分析： 把点代入一次函数，即可求得的值，把点的坐标代入一次函数的，即可求得的值.

求得点的坐标，求出直线BC的解析式，把点的坐标代入，即可判定点B、E、C是否在同一条直线上.

即可求得.

试题解析：

（1）把点A（1，3）代入一次函数，即 解得：

一次函数的解析式为：

把点代入即 解得：

故答案为：4,3.

（2）

∵点E和点D关于对称，

∵点C和点A关于原点对称.

设直线BC的函数的关系式：y=kx+b 将两点代入上式得：

∴直线BC的函数的关系式：

将代入得 则点在直线上，

∴点B、E、C在一条直线上.

（3）