题目内容
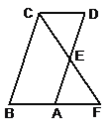
【题目】如图,已知□ABCD中,E为AD的中点,CE的延长线交BA的延长线于点E.
(1)试说明线段CD与FA相等的理由;
(2)若使∠F=∠BCF,□ABCD的边长之间还需再添加一个什么条件?请你补上这个条件,并说明你的理由(不要再增添辅助线).
【答案】见解析
【解析】试题分析:(1)根据平行四边形的性质,-就可证明CD∥AB,∠CDA=∠DAF,又已知DE=AE,∠CED=∠AEF,符合全等三角形的判定中的ASA,即证△CDE≌△AEF,所以CD=AF.
(2)在第(1)问的基础上,若使∠F=∠BCF,逆推就必须BC=BF,继而推出BC=2BA,即为所求.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴CD∥AB.
又∵CE的延长线交BA的延长线于点F,
∴∠CDA=∠DAF.
∵E是AD中点,
∴DE=AE.
∵∠CED=∠AEF,
∴△CDE≌△AEF.
∴CD=AF.
(2)要使∠F=∠BCF,需平行四边形ABCD的边长之间是2倍的关系,即BC=2AB,
证明:∵由(1)知,△CED≌△FEA,
∴CD=AF.
又∵四边形ABCD是平行四边形,
∴CD=AB.
∴AB=AF,即BF=2AB.
∵BC=2AB.
∴BF=BC,
∴∠F=∠BCF.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案【题目】2013年是一个让人记忆犹新的年份,雾霾天气持续笼罩我国大部分地区,口罩市场出现热销,某旗舰网店用8000元购进甲、乙两种型号的口罩,销售完后共获利2800元,进价和售价如下表:
品名 价格 | 甲型口罩 | 乙型口罩 |
进价(元/袋) | 20 | 25 |
售价(元/袋) | 26 | 35 |
(1)求该网店购进甲、乙两种型号口罩各多少袋?
(2)该网店第二次以原价购进甲、乙两种型号口罩,购进乙种型号口罩袋数不变,而购进甲种型号口罩袋数是第一次的2倍.甲种口罩按原售价出售,而乙种口罩让利销售.若两种型号的口罩都售完,要使第二次销售活动获利不少于3680元,乙种型号的口罩最低售价为每袋多少元?
【题目】如图,广宇购物中心设立了一个可以自由转动的转盘,并规定:顾客购物满20元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据.
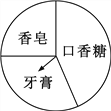
转动转盘的次数n | 100 | 200 | 400 | 500 | 1000 |
落在“牙膏”区域的次数m | 32 | 58 | 121 | 149 | 300 |
落在“牙膏”区域的频率 | 0.3025 |
(1)计算并完成上面的表格;
(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动该转盘一次,你获得牙膏的概率是多少?