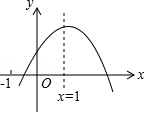题目内容
【题目】如图,已知,A(0,4),B(﹣3,0),C(2,0),D为B点关于AC的对称点,反比例函数y= ![]() 的图象经过D点.
的图象经过D点.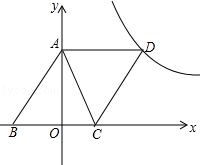
(1)证明四边形ABCD为菱形;
(2)求此反比例函数的解析式;
(3)已知在y= ![]() 的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.
的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.
【答案】
(1)
解:∵A(0,4),B(﹣3,0),C(2,0),
∴OA=4,OB=3,OC=2,
∴AB= ![]() =5,BC=5,
=5,BC=5,
∴AB=BC,
∵D为B点关于AC的对称点,
∴AB=AD,CB=CD,
∴AB=AD=CD=CB,
∴四边形ABCD为菱形
(2)
解:∵四边形ABCD为菱形,
∴D点的坐标为(5,4),反比例函数y= ![]() 的图象经过D点,
的图象经过D点,
∴4= ![]() ,
,
∴k=20,
∴反比例函数的解析式为:y= ![]()
(3)
解:∵四边形ABMN是平行四边形,
∴AN∥BM,AN=BM,
∴AN是BM经过平移得到的,
∴首先BM向右平移了3个单位长度,
∴N点的横坐标为3,
代入y= ![]() ,
,
得y= ![]() ,
,
∴M点的纵坐标为: ![]() ﹣4=
﹣4= ![]() ,
,
∴M点的坐标为:(0, ![]() )
)
【解析】(1)由A(0,4),B(﹣3,0),C(2,0),利用勾股定理可求得AB=5=BC,又由D为B点关于AC的对称点,可得AB=AD,BC=DC,即可证得AB=AD=CD=CB,继而证得四边形ABCD为菱形;(2)由四边形ABCD为菱形,可求得点D的坐标,然后利用待定系数法,即可求得此反比例函数的解析式;(3)由四边形ABMN是平行四边形,根据平移的性质,可求得点N的横坐标,代入反比例函数解析式,即可求得点N的坐标,继而求得M点的坐标.

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案【题目】如图,广宇购物中心设立了一个可以自由转动的转盘,并规定:顾客购物满20元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据.
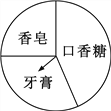
转动转盘的次数n | 100 | 200 | 400 | 500 | 1000 |
落在“牙膏”区域的次数m | 32 | 58 | 121 | 149 | 300 |
落在“牙膏”区域的频率 | 0.3025 |
(1)计算并完成上面的表格;
(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动该转盘一次,你获得牙膏的概率是多少?