题目内容
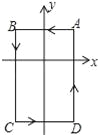
【题目】如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2).把一条长为2012个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣A﹣…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )
A. (1,﹣1) B. (﹣1,1) C. (﹣1,﹣2) D. (1,﹣2)
【答案】B
【解析】根据点的坐标求出四边形ABCD的周长,然后求出另一端是绕第几圈后的第几个单位长度,从而确定答案.
∵A(1,1),B(1,1),C(1,2),D(1,2),
∴AB=1(1)=2,BC=1(2)=3,CD=1(1)=2,DA=1(2)=3,
∴绕四边形ABCD一周的细线长度为2+3+2+3=10,
2012÷10商为201余2,
∴细线另一端在绕四边形第202圈的第2个单位长度的位置,
即点B的位置,点的坐标为(1,1).
故选B.

练习册系列答案
相关题目
【题目】2013年是一个让人记忆犹新的年份,雾霾天气持续笼罩我国大部分地区,口罩市场出现热销,某旗舰网店用8000元购进甲、乙两种型号的口罩,销售完后共获利2800元,进价和售价如下表:
品名 价格 | 甲型口罩 | 乙型口罩 |
进价(元/袋) | 20 | 25 |
售价(元/袋) | 26 | 35 |
(1)求该网店购进甲、乙两种型号口罩各多少袋?
(2)该网店第二次以原价购进甲、乙两种型号口罩,购进乙种型号口罩袋数不变,而购进甲种型号口罩袋数是第一次的2倍.甲种口罩按原售价出售,而乙种口罩让利销售.若两种型号的口罩都售完,要使第二次销售活动获利不少于3680元,乙种型号的口罩最低售价为每袋多少元?