题目内容
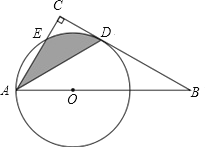
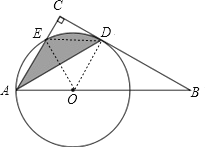
【题目】如图,∠C=90°,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与边BC交于点D,与边AC交于点E,连接AD,且AD平分∠BAC.
(1)求证:BC是⊙O的切线;
(2)若∠BAC=60°,OA=1,求阴影部分的面积(结果保留π).
【答案】(1)BC与O相切,理由见解析;(2) 阴影部分的面积为![]() .
.
【解析】
(1)连接OD,推出OD⊥BC,根据切线的判定推出即可;
(2)连接DE、OE,求出阴影部分的面积=扇形EOD的面积,求出扇形的面积即可.
(1)BC与O相切,
理由:连接OD,
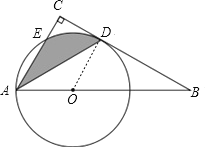
∵AD平分∠BAC,
∴∠BAD=∠DAC,
∵AO=DO,
∴∠BAD=∠ADO,
∴∠CAD=∠ADO,
∴AC∥OD,
∵∠ACD=90,
∴OD⊥BC,
∴BC与O相切;
(2)连接OE,ED,
∵∠BAC=60,OE=OA,
∴△OAE为等边三角形,
∴∠AOE=60,
∴∠ADE=30,
又∵∠OAD=![]() ∠BAC=30,
∠BAC=30,
∴∠ADE=∠OAD,
∴ED∥AO,
![]() 是菱形
是菱形
∴OE⊥AD,且AM=DM,EM=OM
∴![]() S△AED=
S△AED=![]() S△AOD,
S△AOD,
∴阴影部分的面积=S扇形ODE=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目