��Ŀ����
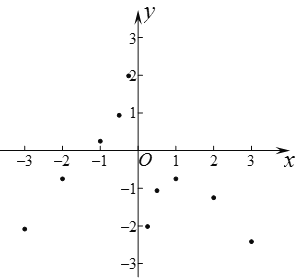
����Ŀ����֪����������y=![]() ��kΪ������k��1����
��k������k��1����
��1����ͼ��������������y=x��ͼ���һ������ΪP������P����������2����k��ֵ��
��2��������ͼ���ÿһ֧�ϣ�y��x���������С����k��ȡֵ��Χ��
��3������ͼ���һ֧λ�ڵڶ����ޣ�����һ֧����ȡ����A��x1��x2����B��x2��y2������y1��y2ʱ���ԱȽ�x1��x2�Ĵ�С��
��4��������ͼ������ȡһ�㣬��x���y�������ߣ������þ������Ϊ6����k��ֵ��
���𰸡���1��k=5����2��k��1����3��x1��x2����4��k=��6��
��������
��1�����P������Ϊ��m��2�����ɵ�P������������y��x��ͼ���Ͽ����m��ֵ�������ó�P���������ٸ��ݵ�P�ڷ���������y![]() ��ͼ�������������k��ֵ��
��ͼ�������������k��ֵ��
��2�������ڷ���������y![]() ͼ���ÿһ֧����y��x���������С����k��1��0�����k��ȡֵ��Χ������
ͼ���ÿһ֧����y��x���������С����k��1��0�����k��ȡֵ��Χ������
��3������������y![]() ͼ���һ֧λ�ڵڶ����������ڸú���ͼ���ÿһ֧����y��x�����������������A��x1��y1�����B��x2��y2���ڸú����ĵڶ�����ͼ��������y1��y2���ʿ�֪x1��x2��
ͼ���һ֧λ�ڵڶ����������ڸú���ͼ���ÿһ֧����y��x�����������������A��x1��y1�����B��x2��y2���ڸú����ĵڶ�����ͼ��������y1��y2���ʿ�֪x1��x2��
��4������k�ļ������弴�ɵó�������
��1�������⣬���P������Ϊ��m��2����
�ߵ�P������������y=x��ͼ���ϣ���2=m����m=2��
���P��������2��2����
�ߵ�P�ڷ���������y=![]() ��ͼ���ϣ���2=
��ͼ���ϣ���2=![]() ����ã�k=5��
����ã�k=5��
��2�����ڷ���������y=![]() ͼ���ÿһ֧�ϣ�y��x���������С����k��1��0����ã�k��1��
ͼ���ÿһ֧�ϣ�y��x���������С����k��1��0����ã�k��1��
��3���߷���������y=![]() ͼ���һ֧λ�ڵڶ����ޣ����ڸú���ͼ���ÿһ֧�ϣ�y��x�����������
ͼ���һ֧λ�ڵڶ����ޣ����ڸú���ͼ���ÿһ֧�ϣ�y��x�����������
�ߵ�A��x1��y1�����B��x2��y2���ڸú����ĵڶ�����ͼ���ϣ���y1��y2 ����x1��x2��
��4��������ͼ������ȡһ�㣬���������������ߣ��õ��ľ���Ϊ6����|k|=6����ã�k=��6��