题目内容
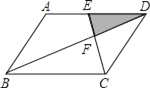
【题目】如图,在矩形![]() 中,
中,![]() 是
是![]() 边的中点,沿
边的中点,沿![]() 对折矩形
对折矩形![]() ,使
,使![]() 点落在
点落在![]() 处,折痕为
处,折痕为![]() ,连接
,连接![]() 并延长
并延长![]() 交
交![]() 于
于![]() 点.
点.
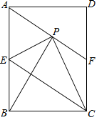
(1)求证:四边形![]() 为平行四边形;
为平行四边形;
(2)若矩形![]() 的边
的边![]() =
=![]() ,
,![]() =
=![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)由折叠的性质得到![]() =
=![]() ,
,![]() 与
与![]() 垂直,根据
垂直,根据![]() 为
为![]() 中点,得到
中点,得到![]() =
=![]() =
=![]() ,利用三角形内一边上的中线等于这条边的一半的三角形为直角三角形,得到
,利用三角形内一边上的中线等于这条边的一半的三角形为直角三角形,得到![]() 为
为![]() ,进而得到
,进而得到![]() 与
与![]() 平行,再由
平行,再由![]() 与
与![]() 平行,利用两对边平行的四边形为平行四边形即可得证;
平行,利用两对边平行的四边形为平行四边形即可得证;
(2)过![]() 作
作![]() ,在直角三角形
,在直角三角形![]() 中,利用勾股定理求出
中,利用勾股定理求出![]() 的长,利用面积法求出
的长,利用面积法求出![]() 的长,根据
的长,根据![]() =
=![]() 求出
求出![]() 的长,在直角三角形
的长,在直角三角形![]() 中,利用勾股定理求出
中,利用勾股定理求出![]() 的长,根据
的长,根据![]() 求出
求出![]() 的长,由
的长,由![]() 与
与![]() 平行,得到三角形
平行,得到三角形![]() 与三角形
与三角形![]() 相似,由相似得比例求出
相似,由相似得比例求出![]() 的长,再由
的长,再由![]() =
=![]() =
=![]() ,求出三角形
,求出三角形![]() 面积即可.
面积即可.
解:(1)由折叠得到![]() =
=![]() ,
,![]() ,
,
∵![]() 为
为![]() 的中点,
的中点,
∴![]() =
=![]() =
=![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴四边形![]() 为平行四边形;
为平行四边形;
(2)过![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,
,
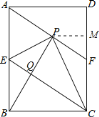
在![]() 中,
中,![]() =
=![]() ,
,![]() =
=![]() ,
,
根据勾股定理得:![]() ,
,
∵![]() ,
,
∴![]() ,
,
由折叠得:![]() =
=![]() ,
,
在![]() 中,
中,![]() =
=![]() ,
,![]() ,
,
根据勾股定理得:![]() ,
,
∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵![]() ,
,
∴![]() ,即
,即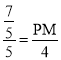 ,
,
解得:![]() ,
,
则![]() .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目