题目内容
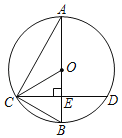
【题目】如图,在△ABC中,D、E分别是边AC、BC的中点,F是BC延长线上一点,∠F=∠B.
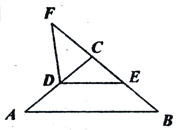
(l)若AB=1O,求FD的长;
(2)若AC=BC.求证:△CDE∽△DFE .
【答案】(1) FD=5; (2)证明见解析.
【解析】试题分析:(1)利用三角形中位线的性质得出DE∥AB,进而得出∠DEC =∠B,即可得出FD=DE,即可得出答案;
(2)利用等腰三角形的性质和平行线的性质得出∠B=∠A=∠CED=∠CDE,即可得出∠CDE=∠F,即可得出△CDE∽△DFE.
试题解析:解:(1)∵D、E分别是AC、BC的中点,∴.DE//AB, DE=![]() AB=5.
AB=5.
又∵DE//AB,∴∠DEC= ∠B.而∠ F= ∠ B,∴∠DEC =∠B,∴FD=DE=5;
(2)∵AC=BC,∴∠A=∠B.又∠CDE=∠A,∠CED= ∠B,∴∠CDE=∠B.
而∠B=∠F,∴∠CDE=∠F,∠CED=∠DEF,∴△CDE∽△DFE .

练习册系列答案
相关题目