题目内容
【题目】如图，在平面直角坐标系中，已知点A、B的坐标分别为（8，0）、（0，2
），C是AB的中点，过点C作y轴的垂线，垂足为D，动点P从点D出发，沿DC向点C匀速运动，过点P作x轴的垂线，垂足为E，连接BP、EC．当BP所在直线与EC所在直线垂直时，点P的坐标为____
【答案】(1, 
)或(3, 
)
【解析】试题分析：由题意可知，OB=2
，AO=8，∵CD⊥BO，C是AB的中点，∴BD=DO=
BO==PE，CD=AO=4.
设DP=a，则CP=4﹣a，当BP所在直线与EC所在直线第一次垂直时，∠FCP=∠DBP，又∵EP⊥CP，PD⊥BD，
∴∠EPC=∠PDB=90°，∴△EPC∽△PDB.∴
=
，∴
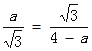，∴a1=1，a2=3（舍去）.∴DP=1，∵PE=，∴P（1，）.
练习册系列答案
相关题目
【题目】抛物线
上部分点坐标如表所示，下列说法错误的是( )
x | … | －3 | －2 | －1 | 0 | 1 | … |
y | … | －6 | 0 | 4 | 6 | 6 | … |
A. 抛物线与y轴的交点为(0，6) B. 抛物线的对称轴是在y轴的右侧；
C. 抛物线一定经过点(3，0) D. 在对称轴左侧，y随x增大而减小．
