题目内容
如图Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值为( )

A.2
| B.2
| C.2
| D.2
|

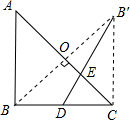
过点B作BO⊥AC于O,延长BO到B′,使OB′=OB,连接DB′,交AC于E,
此时DB′=DE+EB′=DE+BE的值最小.
连接CB′,易证CB′⊥BC,
根据勾股定理可得DB′=
=2
,
则△BDE周长的最小值为2
+2.
故选C.
此时DB′=DE+EB′=DE+BE的值最小.
连接CB′,易证CB′⊥BC,
根据勾股定理可得DB′=
| B′C2+CD2 |
| 5 |
则△BDE周长的最小值为2
| 5 |
故选C.


练习册系列答案
相关题目






