��Ŀ����
����Ŀ����ͼ����P������AB���Ϸ����ҡ�PAB=45�㣬PA=2����M������AB�ϵĶ��㣨��M�����A�غϣ����ֽ���P�Ƶ�A��˳ʱ�뷽����ת60�㣬����Q������M�Ƶ�P����ʱ�뷽����ת60�㵽��N������AQ��PM��PN����ֱ��QN�� 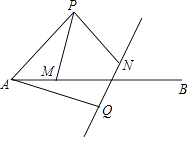
��1����֤��AM=QN��
��2��ֱ��QN���Ե�PΪԲ�ģ���PN�ij�Ϊ�뾶��Բ�Ƿ�������е�����������ڣ��������ʱAM�ij����������ڣ���˵�����ɣ�
��3�����Ե�PΪԲ�ģ���PN�ij�Ϊ�뾶��Բ������Qʱ��ֱ��д���ӻ�NQ�������뾶��Χ�ɵ����ε������
���𰸡�
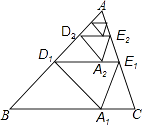
��1��֤������ͼ1������PQ��
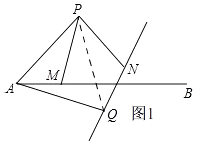
�ɵ�P�Ƶ�A��˳ʱ�뷽����ת60�㵽��Q��
�ɵã�AP=AQ����PAQ=60�㣬
���APQΪ�ȱ������Σ�
��PA=PQ����APQ=60�㣬
�ɵ�M�Ƶ�P����ʱ�뷽����ת60�㵽��N��
�ɵã�PM=PN����MPN=60�㣬
���APM=��QPN��
���APM�ա�QPN��SAS����
��AM=QN
��2���⣺���ڣ�
��ͼ2��
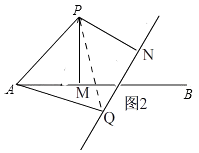
�ɣ�1���е�֤����֪����APM�ա�QPN��
���AMP=��QNP��
��ֱ��QN���Ե�PΪԲ�ģ���PN�ij�Ϊ�뾶��Բ���У�
���AMP=��QNP=90�㣬
����PN��QN��
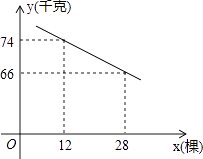
��R��APM�У���PAB=45�㣬PA=2��
��AM= ![]()
��3���⣺��ͼ3��
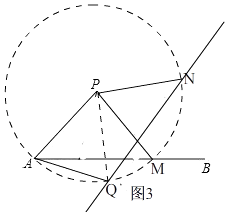
�ɣ�1��֪����APQ�ǵȱ������Σ�
��PA=PQ����APQ=60�㣬
���Ե�PΪԲ�ģ���PN�ij�Ϊ�뾶��Բ������Q��
��PN=PQ=PA��
��PM=PN��
��PA=PM��
�ߡ�PAB=45�㣬
���APM=90�㣬
���MPQ=��APM����APQ=30�㣬
�ߡ�MPN=60�㣬
���QPN=90�㣬
���ӻ�NQ�������뾶��Χ�ɵ����ε����������QPN��������������ε�Բ�Ľǡ�QPN=90�㣬�뾶ΪPN=PM=PA=2��
���ӻ�NQ�������뾶��Χ�ɵ����ε����= ![]() =�У�
=�У�
����������1��������ת����ת�жϳ���APQΪ�ȱ������Σ����жϳ���APM=��QPN���Ӷ��ó���APM�ա�QPN���ɣ���2����ֱ�ߺ�Բ���еó���AMP=��QNP=90�㣬���ù��ɶ�������������ۣ���3�����жϳ�PA=PQ�����жϳ�PQ=PN=PM�����������QPM=30�㣬���������QPN=90�㣬��������ε������ʽ���ɣ�

 Ʒѧ˫�ž�ϵ�д�
Ʒѧ˫�ž�ϵ�д� Сѧ��ĩ���100��ϵ�д�
Сѧ��ĩ���100��ϵ�д� ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д�����Ŀ���ţ�2��������ίԱ�û��Ƿ�ͳ�Ʊ���40��ͬѧͶ��ʵ����ijɼ��������ͼ��ʾ������40��ͬѧͶ��ʵ����ijɼ�����������λ���ֱ��ǣ� ��
�ɼ� | 6 | 7 | 8 | 9 | 10 |
���� |
| �� | �� | �� | �� |
A.8��8
B.8��8.5
C.9��8
D.9��8.5