题目内容
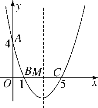
【题目】如图,直线![]() 分别交轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=9.
分别交轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=9.
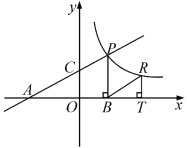
(1)求证:△AOC∽△ABP;
(2)求点P的坐标;
(3)设点R与点P在同一个反比例函数的图象上,且点R在直线PB的右侧,作RT⊥x轴于T,当△BRT与△AOC相似时,求点R的坐标.
【答案】(1)见解析;(2)P为(2,3);(3) R(![]() )或(3,0)
)或(3,0)
【解析】
(1)由一对公共角相等,一对直角相等,利用两对角相等的三角形相似即可证明;
(2)先求点A、C的坐标,再由△AOC∽△ABP,利用线段比求出BP,AB的值即可求出P点坐标;
(3)根据P点求出反比例函数解析式,设R点坐标为(x,y),根据△BRT与△AOC相似分两种情况,利用线段比联立方程组求出x,y的值,即可确定出R坐标.
(1)∵∠CAO=∠PAB,∠AOC=∠ABP=90°,
∴△AOC∽△ABP;
(2)∵直线![]() 分别交轴于A、C
分别交轴于A、C
∴A(-4,0) C(0,2)
∴OA=4,OC=2
∴![]()
∵△AOC∽△ABP,![]()
∴![]() =
=![]() =
=![]()
∴AB=6,PB=3
∴OB=2
∴P为(2,3)
(3)设反比例函数为![]() ,代入P(2,3)得
,代入P(2,3)得![]() ,即
,即![]() ,可设R点为(
,可设R点为(![]() ),则RT=
),则RT=![]() ,TB=
,TB=![]()
①要△BRT∽△ACO,则只要![]() ,即
,即 ,解得
,解得![]()
②若△BRT∽△CAO,则只要![]() ,即
,即 ,解得
,解得![]()
∴R(![]() )或(3
)或(3

练习册系列答案
相关题目