题目内容
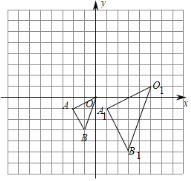
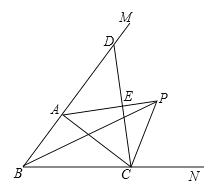
【题目】如图1：在平面直角坐标系内，O为坐标原点，线段AB两端点在坐标轴上且点A（﹣4，0），点B（0，3），将AB向右平移4个单位长度至OC的位置
（1）直接写出点C的坐标 ；
（2）如图2，过点C作CD⊥x轴于点D，在x轴正半轴有一点E（1，0），过点E作x轴的垂线，在垂线上有一动点P，直接写出：①点D的坐标 ； ②三角形PCD的面积为 ；
（3）如图3，在（2）的条件下，连接AC，当△ACP的面积为
时，直接写出点P的坐标 ．
【答案】（1）（4，3）；（2）（4，0）；
；（3）（1，6）或（1，﹣
）．
【解析】
（1）由平移的性质得出点C的横坐标为：0+4=4，纵坐标与点B的相同，即可得出答案；
（2）求出点D的坐标为：（4，0）；求出CD=3，由三角形面积公式即可得出结果；
（3）分两种情况：①当点P在AC的上方时，延长AP、DC交于点H，过点P作PN⊥CH于N，则四边形PEDN是矩形，得出PN=ED=4-1=3，由三角形面积求出CH=
，得出HD=
，则点H的坐标为：（4，），由待定系数法求出直线AH的解析式为：y＝
x+
，即可得出点P的坐标；
②当点P在AC的上方时，延长AP、CD交于点H，过点P作PN⊥CH于N，解法同①．
解：（1）∵线段AB两端点在坐标轴上且点A（﹣4，0），点B（0，3），将AB向右平移4个单位长度至OC的位置，
∴点C的横坐标为：0+4＝4，纵坐标与点B的相同，
∴点C的坐标为：（4，3），
故答案为：（4，3）；
（2）如图2所示：
∵过点C作CD⊥x轴于点D，
∴点D的横坐标与点C的横坐标相同，
∴点D的坐标为：（4，0）；
∵点E（1，0），
∴ED＝3，
∵CD⊥x轴，
∴CD＝3，
∵过点E作x轴的垂线，在垂线上有一动点P，
∴PE∥CD，
∴△PCD的是以CD为底、ED为高，
∴S△PCD＝
CDED＝×3×3＝；
故答案为：（4，0）；；
（3）AD＝4﹣（﹣4）＝8，分两种情况：
①当点P在AC的上方时，如图3所示：
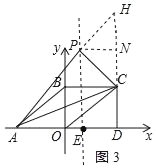
延长AP、DC交于点H，过点P作PN⊥CH于N，则四边形PEDN是矩形，∴PN＝ED＝4﹣1＝3，
∵S△ACP＝S△ACH﹣S△PCH＝ADCH﹣PNCH＝×8×CH﹣×3×CH＝
CH＝
，
∴CH＝，
∴HD＝3+＝，
则点H的坐标为：（4，），
设直线AH的解析式为：y＝kx+a，
则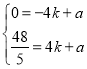
，
解得：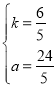
，
∴y＝x+，
∵点P的横坐标x＝1，
∴点P的纵坐标为： +＝6，
∴点P的坐标为：（1，6）；
②当点P在AC的上方时，如图4所示：
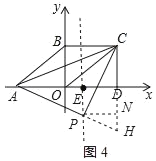
延长AP、CD交于点H，过点P作PN⊥CH于N，则四边形PEDN是矩形，
∴PN＝ED＝4﹣1＝3，
∵S△ACP＝S△ACH﹣S△PCH＝ADCH﹣PNCH＝×8×CH﹣
×3×CH＝CH＝，
∴CH＝，
∴HD＝﹣3＝
，
则点H的坐标为：（4，﹣），
设直线AH的解析式为：y＝kx+a，
则：
，
解得：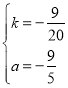
，
∴y＝﹣
x﹣
，
∵点P的横坐标x＝1，
∴点P的纵坐标为：﹣﹣＝﹣，
∴点P的坐标为：（1，﹣）；
综上所述，点P的坐标为：（1，6）或（1，﹣）．；
故答案为：（1，6）或（1，﹣）．
