Question

23、如图，四边形ABCD是正方形，CE是∠BCD的外角∠DCF的平分线．

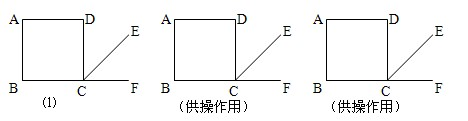
（如果需要，还可以继续操作、实验与测量）
（1）操作实验：将直角尺的直角顶点P在边BC上移动（与点B、C不重合），且一直角边经过点A，另一直角边与射线CE交于点Q，不断移动P点，同时测量线段PQ与线段PA的长度，完成下列表格（精确到0.1cm）．

（2）观测测量结果，猜测它们之间的关系：

PA=PQ

；
（3）对你猜测的结论是否成立均进行说明理由；
（4）当点P在BC的延长线上移动时，继续（1）的操作实验，试问：（1）中的猜测结论还成立吗？若成立，请给出理由；若不成立，也请说明理由．

Answer 1

分析：（1）根据测量方法进行测量即可；
（2）通过观察测量可知它们之间的关系：PA=PD；
（3）利用三角形全等的条件证得△AGP≌△PCQ，所以得到AP=QP；
（4）证明方法同（3）．

解答：解：（1）答案不唯一，只要测出的PA=PD即可；
（2）观测测量结果，猜测它们之间的关系：PA=PD；
（3）证明：在AB是截取BP=BG，则AG=PC，
∵∠AGP=180-45=135°，∠PCQ=90°+45°=135°，
∴∠AGP=∠PCQ，
∵∠APB+∠BAP=90°，∠APB+∠CPQ=90°，
∴∠GAP=∠CPQ，
∴△AGP≌△PCQ，
∴AP=QP；
（4）成立，证明方法同（3）．

点评：主要考查了正方形的性质．要掌握正方形中一些特殊的性质：四边相等，四角相等，对角线相等且互相平分．利用这些等量关系求得三角形全等是解题的关键．