题目内容
【题目】如图,在四边形ABCD中,AC=BD,M,N分别是AB,CD的中点,MN分别交BD和AC于点E,F,对角线AC和BD相交于点G,则GE和GF相等吗?为什么?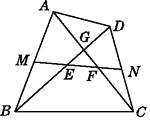
【答案】解:GE=GF.理由如下:
取BC的中点P,连接MP,NP.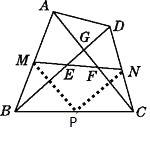
∵AM=BM,BP=CP,
∴MP∥AC,MP= ![]() AC.
AC.
同理NP∥BD,NP= ![]() BD.
BD.
∵AC=BD,∴MP=NP.
∴∠PMN=∠PNM.
∵MP∥AC,NP∥BD,
∴∠GFE=∠PMN,∠GEF=∠PNM.
∴∠GFE=∠GEF.
∴GE=GF.
【解析】根据已知条件M,N分别是AB,CD的中点,取BC的中点P,连接MP,NP,构造△ABC和△BCD的中位线,根据中位线定理及AC=BD,证出MP=NP,再根据等边对等角得出∠PMN=∠PNM,然后根据平行线的性质证得∠GFE=∠PMN,∠GEF=∠PNM,得出∠GFE=∠GEF,根据等角对等边可证得结论。

 孟建平名校考卷系列答案
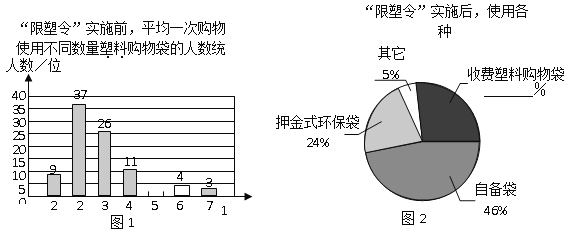
孟建平名校考卷系列答案【题目】为减少环境污染,自2008年6月1日起,全国的商品零售场所开始实行“塑料购物袋有偿使用制度”(以下简称“限塑令”).某班同学于6月上旬的一天,在某超市门口采用问卷调查的方式,随机调查了“限塑令”实施前后,顾客在该超市用购物袋的情况,以下是根据100位顾客的100份有效答卷画出的统计图表的一部分:
“限塑令”实施后,塑料购物袋使用后的处理方式统计表
处理方式 | 直接丢弃 | 直接做垃圾袋 | 再次购物使用 | 其它 |
选该项的人数占 总人数的百分比 | 5% | 35% | 49% | 11% |
请你根据以上信息解答下列问题:
(1)补全图1,“限塑令”实施前,如果每天约有2 000人次到该超市购物.根据这100位顾客平均一次购物使用塑料购物袋的平均数,估计这个超市每天需要为顾客提供多少个塑料购物袋?
(2)补全图2,并根据统计图和统计表说明,购物时怎样选用购物袋,塑料购物袋使用后怎样处理,能对环境保护带来积极的影响.