题目内容
【题目】如图,四边形ABCD为矩形,O为AC中点,过点O作AC的垂线分别交AD、BC于点E、F,连接AF、CE.
(1)求证:四边形AFCE是菱形;
(2)若AC=8,EF=6,求BF的长.

【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)由条件可先证四边形![]() 为平行四边形,再结合线段垂直平分线的性质可证得结论;
为平行四边形,再结合线段垂直平分线的性质可证得结论;
(2)由菱形的性质可求得![]() 设
设![]() 在
在![]() 和
和![]() 中,分别利用勾股定理可得到关于
中,分别利用勾股定理可得到关于![]() 的方程,可求得
的方程,可求得![]() 的长.
的长.
试题解析:∵O为AC中点,EF⊥AC,
∴EF为AC的垂直平分线,
∴EA=EC,FA=FC,
∴∠EAC=∠ECA,∠FAC=∠FCA.
![]()
∴∠EAC=∠FCA,
∴∠FAC=∠ECA,
![]()
∴四边形AFCE平行四边形。
又∵EA=EC,
∴平行四边形AFCE是菱形。
(2)∵四边形AFCE是菱形,AC=8,EF=6,
∴OE=3,OA=4,
∴AE=CF=5,
设BF=x,
在![]() 中,
中, ![]() 在
在![]() 中,
中, ![]()
![]()
解得![]()
![]()

【题目】已知,在一个盒子里有红球和白球共10个,它们除颜色外都相同,将它们充分摇匀后,从中随机抽出一个,记下颜色后放回.在摸球活动中得到如下数据:
摸球总次数 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
摸到红球的频数 | 17 | 32 | 44 | 64 | 78 |
| 103 | 122 | 136 | 148 |
摸到红球的频率 | 0.34 | 0.32 | 0.293 | 0.32 | 0.312 | 0.32 | 0.294 |
| 0.302 |
|
(1)请将表格中的数据补齐;
(2)根据上表,完成折线统计图;
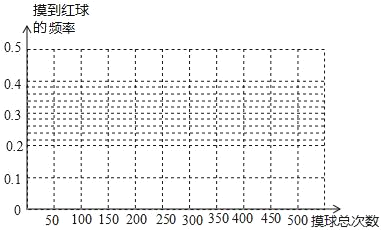
(3)请你估计,当摸球次数很大时,摸到红球的频率将会接近 (精确到0.1).
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按x元/公里计算,耗时费按y元/分钟计算(总费用不足9元按9元计价).小明、小刚两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程数与打车时间如表:
时间(分钟) | 里程数(公里) | 车费(元) | |
小明 | 8 | 8 | 12 |
小刚 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小华也用该打车方式,打车行驶了11公里,用了14分钟,那么小华的打车总费用为多少?