题目内容
【题目】如图,在正方形网格中,△TAB顶点坐标分别为T(1,1)、A(2,3)、B(4,2).
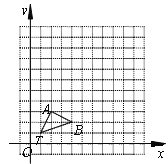
(1)以点T(1,1)为位似中心,按比例尺(TA′∶TA)3∶1在位似中心的同侧将△TAB放大为△TA′B′,放大后点A、B的对应点分别为A′、B′.画出△TA′B′,并写出点A′、B′的坐标;
(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标.
【答案】(1)
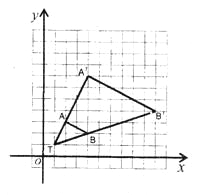
A′(4,7),B′(10,4)
(2)C′(3a-2,3b-2)
【解析】试题分析:(1)依题意知,以点T(1,1)为位似中心,按比例尺(TA′:TA)3:1的位似中心的同侧将TAB放大为△TA′B′,故TA’=3TA,B’T=3BT。则延长如图,连结A’B’得△TA′B′。
由图可得A′坐标为(4,7),B′坐标为(10,4);
(2) 易知A、B坐标由A(2,3),B(4,2)变化为A′(4,7),B′(10,4);
则x值变化=3x-2,y值变化=3y-2;
若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标,则变化后点C的对应点C′的坐标为:C′(3a-2,3b-2)

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目