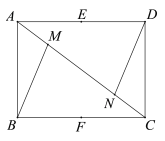
��Ŀ����
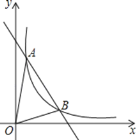
����Ŀ����D�ǵȱߡ�ABC(�������߶���ȣ������Ƕ���ȵ�������)��BA������һ��(��D���B���غ�)������DC��
(1)��ͼ1����DCΪ����BC�Ϸ����ȱߡ�DCF������AF�������߶�AF��BD��������ϵ����˵�����ɣ�
(2)��ͼ2������DCΪ����BC�Ϸ����·��ֱ����ȱߡ�DCF�͵ȱߡ�DCF�䣬����AF��BF�䣬̽��AF��BF����AB�к�������ϵ����˵�����ɣ�

���𰸡�(1)BD��AF�����ɼ�������(2)AB��AF+BF�䣬���ɼ�����.
��������
��1��֤����BCD�ա�ACF�����ɵó����ۣ���2��֤����F��CB�ա�DCA���õ�BF����DA�����ɣ�1�����ɵõ�����.
(1)BD��AF��
���ɣ��ߡ�ABC�͡�DCF���ǵȱ������Σ�
��BC��AC��CD��CF����ACB����DCF��60�㣬
���BCD����ACF��
�ڡ�BCD�͡�ACF�У�
 ��
��
���BCD�ա�ACF(SAS)��
��BD��AF��
(2)AB��AF+BF�䣬
���ɣ��ߡ�ABC�͡�DCF���ǵȱ������Σ�
��BC��AC��CF�䣽CD����F��CD����BCA��60�㣬
���F��CB����DCA��
�ڡ�F��CB�͡�DCA�У�
 ��
��
���F��CB�ա�DCA(SAS)��
��BF�䣽DA��
��(1)֪��BD��AF��
��AB��BD+AD��
��AB��AF+BF�䣮

 һ������ϵ�д�
һ������ϵ�д� �Ƹ�С״Ԫ���ֳ������ϵ�д�
�Ƹ�С״Ԫ���ֳ������ϵ�д� �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д� ����ͬѧһ����ʦȫ�źþ�ϵ�д�
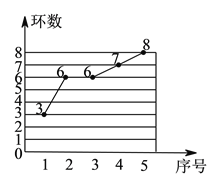
����ͬѧһ����ʦȫ�źþ�ϵ�д�����Ŀ��������Ӽס��������˶�Ա��ѡ��һ�˲μ����������������������Ӿ�����һ��ѡ�α���������ͬ�������¸����![]() �Σ�ÿ����еijɼ������ͼ��ʾ��
�Σ�ÿ����еijɼ������ͼ��ʾ��
����гɼ�������ͳ��ͼ
| ����гɼ�������ͳ��ͼ
|
��![]() ���������ͼ�е�������д�±���
���������ͼ�е�������д�±���
ƽ���� | ���� | ���� | |
�� | __________ |
|
|
�� |
| __________ | __________ |
��![]() ������ѡ�������������ѡ���˼��˶�Ա�μ��������������������ͣ�
������ѡ�������������ѡ���˼��˶�Ա�μ��������������������ͣ�