题目内容
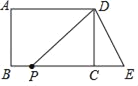
【题目】如图,在长方形ABCD中,AB=6厘米,AD=8厘米.延长BC到点E,使CE=3厘米,连接DE.动点P从B点出发,以2厘米/秒的速度向终点C匀速运动,连接DP.设运动时间为t秒,解答下列问题:
(1)当t为何值时,△PCD为等腰直角三角形?
(2)设△PCD的面积为S(平方厘米),试确定S与t的关系式;
(3)当t为何值时,△PCD的面积为长方形ABCD面积的![]() ?
?
(4)若动点P从点B出发,以2厘米/秒的速度沿BC﹣CD﹣DA向终点A运动,是否存在某一时刻t,使△ABP和△DCE全等?若存在,请求出t的值;若不存在,请说明理由.
【答案】(1)t=1秒;(2)S=﹣6t+24(0≤t≤4);(3)t=2秒;(4)t=![]() 秒或
秒或![]() 秒时,△ABP和△DCE全等.
秒时,△ABP和△DCE全等.
【解析】
(1)用含t的式子表示PC,再根据△CDP是等腰直角三角形得到CP=CD=6,解出t即可;(2)利用S△PCD=![]() CP×CD即可求解;(3)根据面积的关系即可列式求解;(4)根据对应点不同分两种情况讨论即可求解.
CP×CD即可求解;(3)根据面积的关系即可列式求解;(4)根据对应点不同分两种情况讨论即可求解.
(1)在长方形ABCD中,AB=6厘米,AD=8厘米,
∴BC=AD=8cm,CD=AB=6cm,∠DCB=∠DCE=90°,
由运动知,BP=2t,
∴PC=BC﹣BP=8﹣2t,
∴△CDP是等腰直角三角形,
∴CP=CD=6,
∴8﹣2t=6,
∴t=1秒,
(2)由(1)知,PC=8﹣2t,
∴S=S△PCD=![]() CP×CD=
CP×CD=![]() (8﹣2t)×6=﹣6t+24(0≤t≤4);
(8﹣2t)×6=﹣6t+24(0≤t≤4);
(3)∵AB=6,AD=8,
∴S长方形ABCD=6×8=48cm2,
由(2)知,S=﹣6t+24(0≤t≤4),
∵△PCD的面积为长方形ABCD面积的![]() ,
,
∴﹣6t+24=![]() ×48,
×48,
∴t=2秒,
(4)在△ABP中,AB=6cm,在△CDE中,CD=6cm,
∴AB=CD,
∵△ABP和△DCE全等,
∴△ABP≌△DCE或△ABP≌△CDE,
当△ABP≌△DCE时,BP=CE=3,
∴2t=3,
∴t=![]() ,
,
当△ABP≌△CDE时,AP=CE=3,
∴8+6+8﹣2t=3,
∴t=![]() ,
,
即:t=![]() 秒或
秒或![]() 秒时,△ABP和△DCE全等.
秒时,△ABP和△DCE全等.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案