题目内容
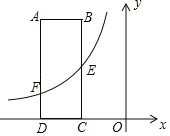
【题目】如图,在直角坐标系![]() 中,矩形
中,矩形![]() 的
的![]() 边在
边在![]() 轴上,
轴上,![]() 点坐标为
点坐标为![]() 边
边![]() 、
、![]() 的长分别为3、8,
的长分别为3、8,![]() 是
是![]() 的中点,反比例函数
的中点,反比例函数![]() 的图象经过点
的图象经过点![]() ,与
,与![]() 边交于点
边交于点![]() .
.
(1)求![]() 的值及经过
的值及经过![]() 、
、![]() 两点的一次函数的表达式;
两点的一次函数的表达式;
(2)若![]() 轴上有一点
轴上有一点![]() ,使
,使![]() 的值最小,试求出点
的值最小,试求出点![]() 的坐标;
的坐标;
(3)在(2)的条件下,连接![]() 、
、![]() 、
、![]() ,在直线
,在直线![]() 上找一点
上找一点![]() ,使得
,使得![]() 直接写出符合条件的
直接写出符合条件的![]() 点坐标.
点坐标.
【答案】(1)k=12,一次函数的表达式为:y=![]() x;(2)P(5,0);(3)(
x;(2)P(5,0);(3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)先确定出点B,C坐标,进而得出点E坐标,最后用待定系数法,即可求出直线AE解析式;
(2)先找出点F关于x轴的对称点F'的坐标,进而求出直线EF'的解析式,即可得出结论;
(3)先利用面积和差求出三角形PEF的面积,再求出直线EF的解析式,设出点Q的坐标,过点Q作y轴的平行线交直线EF于G,表示出点G的坐标,利用坐标系中求三角形面积的方法建立方程求解,即可得出结论.
(1)在矩形ABCD中,AB=3,AD=8,
∴CD=AB=3,BC=AD=8,
∵D(6,0),
∴A(6,8),C(3,0),B(3,8),
∵E是BC的中点,
∴E(3,4),
∵点E在反比例函数![]() 的图象上,
的图象上,
∴k=3×4=12,
设经过A、E两点的一次函数的表达式为:y=ax+b,
∴![]() ,解得:
,解得: ,
,
∴经过A.、E两点的一次函数的表达式为:y=![]() x;
x;
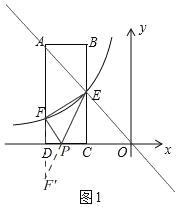
(2)如图1,由(1)可知,k=12,
∴反比例函数的解析式为:![]() ,
,
∵点F的横坐标为6,
∴点F的纵坐标为2,
∴F(6,2),
作点F关于x轴的对称点F′,则F′(6,2),
连接EF′交x轴于P,此时,PE+PF的值最小,
∵E(3,4),
∴由待定系数法可得:直线EF′的解析式为:y=2x+10,
令y=0,则2x+10=0,
∴x=5,
∴P(5,0);
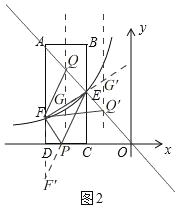
(3)如图2,由(2)知,F′(6,2),
∵E(3,4),F(6,2),
∴S△PEF=S△EFF′S△PFF′=![]() ×(2+2)×(3+6)
×(2+2)×(3+6) ![]() ×(2+2)×(5+6)=4,
×(2+2)×(5+6)=4,
∵E(3,4),F(6,2),
∴由待定系数法得:直线EF的解析式为:y=![]() x+6,
x+6,
由(1)知,经过A.、E两点的一次函数的表达式为:y=![]() x,
x,
设点Q(m,![]() m),
m),
过点Q作y轴的平行线交直线EF于G,
∴G(m,![]() m+6),
m+6),
∴QG=|![]() m
m![]() m6|=|2m+6|,
m6|=|2m+6|,
∵S△QEF=S△PEF,
∴S△QEF=![]() |2m+6|×(3+6)=4,
|2m+6|×(3+6)=4,
∴m=![]() 或m=
或m=![]() ,
,
∴Q(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案