Question

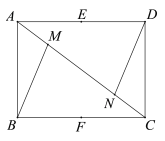
【题目】如图，在矩形ABCD中，AB=3，BC=4．M、N在对角线AC上，且AM=CN，E、F分别是AD、BC的中点．

（1）求证：△ABM≌△CDN；

（2）点G是对角线AC上的点，∠EGF=90°，求AG的长．

Answer 1

【答案】（1）见解析；（2）AG的长为1或4．

【解析】

（1）根据四边形的性质得到AB∥CD，求得∠MAB=∠NCD．根据全等三角形的判定定理得到结论；
（2）连接EF，交AC于点O．根据全等三角形的性质得到EO=FO，AO=CO，于是得到结论．

（1）证明∵四边形ABCD是矩形，∴AB∥CD，∴∠MAB = ∠NCD．

在△ABM和△CDN中，

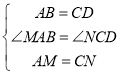
∴△ABM≌△CDN；

（2）解：如图，连接EF，交AC于点O．

在△AEO和△CFO中，

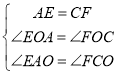
∴△AEO≌△CFO，∴EO=FO，AO=CO，∴O为EF、AC中点．

∵∠EGF=90°，，∴AG=OA-OG =1或AG=OA+OG=4，

∴AG的长为1或4．