题目内容
已知抛物线
的顶点在x轴上，且与y轴交于A点. 直线
经过A、B两点，点B的坐标为（3，4）.
（1）求抛物线的解析式，并判断点B是否在抛物线上；
（2）如果点B在抛物线上，P为线段AB上的一个动点（点P与A、B不重合），过P作x轴的垂线与这个二次函数的图象交于点E，设线段PE的长为h，点P的横坐标为x.当x为何值时，h取得最大值，求出这时的h值.
（1) 不在；（2）当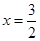
时，h有最大值
.
解析试题分析：（1)∵抛物线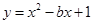
的顶点在x轴上，
∴
.
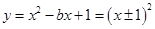∴b=±2.
∴抛物线的解析式为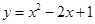
或
将B（3，4）代入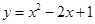，左=右，
∴点B在抛物线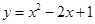上.
将B（3，4）代入，左≠右，
∴点B不在抛物线上
（2）∵A点坐标为（0，1），点B坐标为（3，4），直线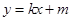
过A、B两点
∴
.∴
∴
.
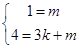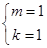
∵点B在抛物线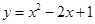上.
设P、E两点的纵坐标分别为yP和yE .
∴ PE=h=yP－yE
=(x+1)－(x2－2x+1)
=－x2+3x.
即h=x2+3x(0＜x＜3).
∴当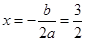
时，h有最大值
最大值为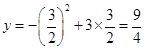
.
考点：二次函数综合题．
练习册系列答案
名校课堂系列答案
相关题目
过点（2，-2）和（-1，10），与x轴交于A、B两点，与y轴交于C点．
与x轴相交于点A,与直线
相交于点P.动点E从原点O出发,以每秒1个单位长度的速度沿着OPA的路线向点A匀速运动（E不与点O,A重合）,过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分面积为S.
二次函数y=x2+bx+c的图象经过点（4,3）,（3,0）．
（1）b= ,c= ；
（2）选取适当的数据填写下表,并在右图的直角坐标系中画出该函数的图像；
| x | … | | | | | | … |
| y | … | | | | | | … |
（3）若将此图象沿x轴向左平移3个单位,直接写出平移后图象所对应的函数关系式 .
（
）．
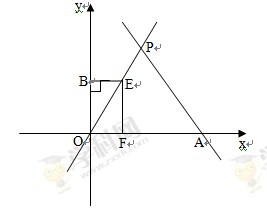
轴的交点坐标；
的值；
的图象与抛物线始终只有一个公共点,求一次函数的解析式.
，抛物线
过A、B两点.
