题目内容
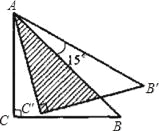
【题目】如图，将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′，若AC=1，则图中阴影部分的面积为（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
设B′C′与AB交点为D，根据等腰直角三角形的性质求出∠BAC=45°，再根据旋转的性质求出∠CAC′=15°，AC′=AC，然后求出∠C′AD=30°，再根据直角三角形30°角所得到直角边等于斜边的一半可得AD=2C′D，然后利用勾股定理列式求出C′D，再利用三角形的面积公式列式进行计算即可得解．
如图，设B′C′与AB交点为D，
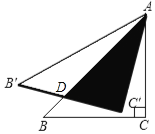
∵△ABC是等腰直角三角形，
∴∠BAC=45°，
∵△AB′C′是△ABC绕点A逆时针旋转15°后得到，
∴∠CAC′=15°，AC′=AC=1，
∴∠C′AD=∠BAC﹣∠CAC′=45°﹣15°=30°，
∵AD=2C′D，
∴AD2=AC′2+C′D2，
即（2C′D）2=12+C′D2，
解得C′D=
，
故阴影部分的面积=
．
故选B．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
【题目】某产品每件成本10元，试销阶段每件产品的销售单价x（元/件）与日销售量y（件）之间的关系如下表．
x（元∕件） | 15 | 18 | 20 | 22 | … |
y（件） | 250 | 220 | 200 | 180 | … |
按照这样的规律可得，日销售利润w（元）与销售单价x（元/件）之间的函数关系式是 ．
