题目内容
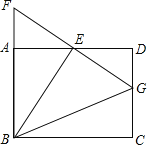
【题目】如图1，BD是正方形ABCD的对角线，BC=4，点H是AD边上的一动点，连接CH，作
，使得HE=CH，连接AE。
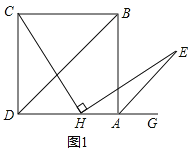
（1）求证：
；
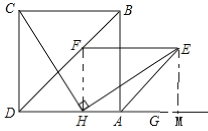
（2）如图2，过点E作EF//AD交对角线BD于点F，试探究：在点H的运动过程中，EF的长度是否为一个定值；如果是，请求出EF的长度。
【答案】（1）见解析（2）EF为定值4
【解析】
（1）根据CH⊥HE与正方形的内角为90°即可证明；
（2）连接FH，作EM⊥AG延长线，可证明四边形EFHM为矩形，再得到EF=HM=DC即可求解.
（1）∵CH⊥HE
∴∠CHD+∠AHE=90°，
又∠DCH+∠CHD=90°，
∴
（2）连接FH，作EM⊥AG延长线，
∵EF//AD，FH⊥DA，∴四边形EFHM为矩形
∴EF=HM
∵CH=HE，，又∠CDH=∠HME=90°，
∴△CDH≌△HME
∴HM=CD，
故EF=CD=4为定值.
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
