题目内容
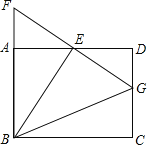
【题目】如图所示,等边三角形![]() 沿射线
沿射线![]() 向右平移到
向右平移到![]() 的位置,连接
的位置,连接![]() 、
、![]() ,则下列结论:(1)
,则下列结论:(1)![]() (2)
(2)![]() 与
与![]() 互相平分(3)四边形
互相平分(3)四边形![]() 是菱形(4)
是菱形(4)![]() ,其中正确的个数是( )
,其中正确的个数是( )
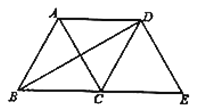
A. 1B. 2C. 3D. 4
【答案】D
【解析】
先求出∠ACD=60°,继而可判断△ACD是等边三角形,从而可判断①是正确的;根据①的结论,可判断四边形ABCD是平行四边形,从而可判断②是正确的;再结合①的结论,可判断③正确;根据菱形的对角线互相垂直可得AC⊥BD,再根据平移后对应线段互相平行可得∠BDE=∠COD=90°,进而判断④正确.
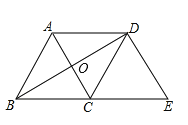
解:如图:∵△ABC,△DCE是等边三角形
∴∠ACB=∠DCE=60°,AC=CD
∴∠ACD=180°-∠ACB-∠DCE=60°
∴△ACD是等边三角形
∴AD=AC=BC,故①正确;
由①可得AD=BC
∵AB=CD
∴四边形ABCD是平行四边形,
∴BD、AC互相平分,故②正确;
由①可得AD=AC=CE=DE故四边形ACED是菱形,即③ 正确
∵四边形ABCD是平行四边形,BA=BC
∴.四边形ABCD是菱形
∴AC⊥BD,AC//DE
∴∠BDE=∠COD=90°
∴BD⊥DE,故④正确
综上可得①②③④正确,共4个.
故选:D

练习册系列答案
相关题目