题目内容
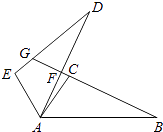
【题目】如图,△ABC中,AB=AC,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,则下列五个结论:①AD上任意一点到AB,AC两边的距离相等;②AD上任意一点到B,C两点的距离相等;③AD⊥BC,且BD=CD;④∠BDE=∠CDF;⑤AE=AF.其中,正确的有( ) 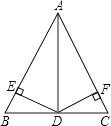
A.2个
B.3个
C.4个
D.5个
【答案】D
【解析】解:∵AB=AC
∴△ABC是等腰三角形,∠B=∠C
∵AD平分∠BAC,DE⊥AB于E,DF⊥AC于F
∴AD⊥BC,BD=CD,DE=DF,故③正确;
∴②正确;
∴AD是BC的中垂线
∴①正确;
∵DE⊥AB于E,DF⊥AC
∴∠=∠DFC=90°
∵∠=∠DFC=90°,BD=CD,∠B=∠C
∴△BED≌△CFD
∴∠BDE=∠CDF,即④正确;
∵∠AED=∠AFD=90°,AD=AD,∠EAD=∠FAD
∴△AED≌△AFD
∴AE=AF,故⑤正确.
故选D.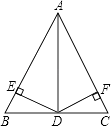
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)).

练习册系列答案
相关题目