��Ŀ����
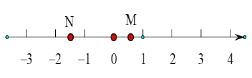
����Ŀ����֪����ʽ4x6y2- 3x2y- x- 7��������b��4a��b��Ϊ�෴�����������ϣ���A��ʾ��a����B��ʾ��b��
��1��a=____________��b=____________
��2����С���ϼ״ӵ�A����3����λ����/����ٶ������˶���ͬʱС�����Ҵӵ�B����4��λ����/����ٶ�Ҳ�����˶�����ͬѧ�۲���ֻС�����˶��������Ǹտ�ʼ�˶�ʱ����ԭ��0������һ�ŷ��������������������������ŷ�����ԭ�����ٶ����෴�ķ����˶������˶���ʱ��Ϊt�룬��ס�����ֻС���ϵ�ԭ��ľ������ʱ����Ӧ��ʱ��t����д�������̣�
��3����С���ϼ���Լ�÷ֱ��A��B���㣬�ֱ����������������������ͬ���ٶ����У�����һ��ʱ��ԭ·���أ��պ���16sʱһ�����»ص�ԭ������A��B����С�����dz���t��s��ʱ���ٶ�Ϊv��mm/s����v��t֮��Ĺ�ϵ����ͼ��������s��ʾʱ�䵥λ�룬mm��ʾ·�̵�λ���ף�
t ��s�� | 0<t��2 | 2<t��5 | 5<t��16 |
v��mm/s�� | 10 | 16 | 8 |
�ٵ�2<t��5ʱ����֪��С���ϼ�����֮��ľ����𣿣��ú���t�Ĵ���ʽ��ʾ����
�ڵ�tΪ__________________ʱ��С���ϼ���֮��ľ�����42mm������ֱ��д���𰸣�
![]()
���𰸡���1��a=-2��b=8����2��10����![]() ����3����32t-14����1.6���14��.
����3����32t-14����1.6���14��.
��������
��1�����ݶ���ʽ�Ĵ�������ɵ�bֵ�������෴���Ķ���ɵ�aֵ��
��2��������������ۣ��ټס�����С���Ͼ������˶�����0��t��2ʱ���ڼ������˶����������˶�ʱ����t��2ʱ.�ֱ��з�����⼴�ɣ�
��3�����ȼ����С���ϼ��Ҹ������е���·�̣��ݴ��жϵ�2<t��5ʱ��С���ϼ���û���п�ʼ����,��ʽ��⼴�ɣ�
���ȼ����С���ϼ��ҿ�ʼ���̵�ʱ��Ϊ��![]() ��ʱ, Ȼ�������������ۣ���0<t��2ʱ����2<t��5ʱ����5<t��
��ʱ, Ȼ�������������ۣ���0<t��2ʱ����2<t��5ʱ����5<t��![]() ʱ����
ʱ����![]() <t��16ʱ���ֱ��з�����⼴��.
<t��16ʱ���ֱ��з�����⼴��.
�⣺��1���߶���ʽ4x6y2- 3x2y- x- 7������8��
��b=8��
��4a��b��Ϊ�෴����
��4a =-8��
��a =-2��
�ʴ��ǣ�-2��8.
��2��������������ۣ�
�ټס�����С���Ͼ������˶�����0��t��2ʱ����ʱOA=2+3t��OB=8-4t��
��OA=OB��
��2+3t=8-4t
��ã�t=![]() ��
��
�ڼ������˶����������˶�ʱ����t��2ʱ��
��ʱOA=2+3t��OB=4t-8��
������ã�2+3t=4t-8��
��ã�t=10��
�𣺼ס�����С���ϵ�ԭ��ľ������ʱ������ʱ����![]() ���10�룮
���10�룮
��3���١�С���ϼ���ͬʱ��������ͬ���ٶ����У�
��С���ϼ������е�·������ͬ�ģ��������е���·�̶�����
10��2+16��3+8��11=156��mm����
��ԭ·���أ��պ���16sʱһ�����»ص�ԭ������A��B��
��С���ϼ��ҷ��̵�·�̶�����78mm,
�൱2<t��5ʱ��С���ϼ���û���п�ʼ����,
�������֮��ľ���=8-(-2)+ 10��2��2+16��(t-2) ��2= 32t-14,
����a����С���ϼ��ҿ�ʼ����,�ɣ�3����֪5<a��16��
��10��2+16��3+8����a-5��=78��
��a=![]() .
.
���������������ۣ�
��0<t��2ʱ��С���ϼ���û���п�ʼ���̣�
8-(-2)+ 10��t��2= 42,
��ã�t=1.6��
��2<t��5ʱ��С���ϼ���û���п�ʼ���̣�
32t-14=42,
��ã�t=![]() <2���������⣬��ȥ��
<2���������⣬��ȥ��
��5<t��![]() ʱ��С���ϼ���û���п�ʼ���̣���2<t��5ʱ�������֪����ʱС���ϼ���֮��ľ������42mm�����Բ������⣻
ʱ��С���ϼ���û���п�ʼ���̣���2<t��5ʱ�������֪����ʱС���ϼ���֮��ľ������42mm�����Բ������⣻
��![]() <t��16ʱ��С���ϼ��ҿ�ʼ���̣�
<t��16ʱ��С���ϼ��ҿ�ʼ���̣�
8-(-2)+ 78��2-8����t-![]() ����2= 42,
����2= 42,
��ã�t=14��
������������t=1.6���14��ʱ��С���ϼ���֮��ľ�����42mm��
�ʴ��ǣ�1.6���14��.