题目内容
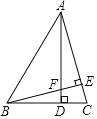
【题目】探究与发现:如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D在底边BC上,AE=AD,连结DE.

(1)当∠BAD=60°时,求∠CDE的度数;
(2)当点D在BC (点B、C除外) 上运动时,试猜想并探究∠BAD与∠CDE的数量关系.
【答案】(1)∠EDC=30°.(2)∠CDE =![]() ∠BAD.理由见解析.
∠BAD.理由见解析.
【解析】
(1)先根据等腰直角三角形的性质得到∠B=∠C=45°,根据三角形外角的性质和已知各角的度数得出∠ADC=∠B+∠BAD=105°,再根据三角形外角的性质得到∠AED=∠C+∠EDC,则结合题意可得∠ADC-∠EDC=105°-∠EDC=45°+∠EDC,解得∠EDC=30°.
(2)由AE=AD,得到∠ADE=∠AED,设∠BAD=x.根据三角形外角的性质得到∠ADC=∠B+∠BAD=45°+x和∠AED=∠C+∠EDC,结合题意得到∠EDC=![]() ∠BAD.
∠BAD.
(1)∵在Rt△ABC中,∠BAC=90°,AB=AC,
则∠B=∠C=45°,
又∵∠ADC是△ABD的外角,∠BAD=60°,
∴∠ADC=∠B+∠BAD=105°.
∵∠AED是△CDE的外角,
∴∠AED=∠C+∠EDC.
∵∠B=∠C,∠ADE=∠AED,
∴∠ADC-∠EDC=105°-∠EDC=45°+∠EDC,
解得:∠EDC=30°.
(2)∠CDE=![]() ∠BAD.
∠BAD.
理由如下:
∵AE=AD,
则∠ADE=∠AED,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=45°+∠BAD
∵∠AED是△CDE的外角,
∴∠AED=∠EDC +∠C=∠EDC+45°,
∵∠B=∠C=45°,∠ADE=∠AED,
∴∠ADE=∠ADC-∠EDC=45°+∠BAD-∠EDC=45°+∠EDC,
解得:∠EDC =![]() ∠BAD,.故∠CDE=
∠BAD,.故∠CDE=![]() ∠BAD.
∠BAD.

【题目】已知多项式4x6y2- 3x2y- x- 7,次数是b,4a与b互为相反数,在数轴上,点A表示数a,点B表示数b.
(1)a=____________,b=____________
(2)若小蚂蚁甲从点A处以3个单位长度/秒的速度向左运动,同时小蚂蚁乙从点B处以4单位长度/秒的速度也向左运动,丙同学观察两只小蚂蚁运动,在它们刚开始运动时,在原点0处放置一颗饭粒,乙在碰到饭粒后立即背着饭粒以原来的速度向相反的方向运动,设运动的时间为t秒,求甲、乙两只小蚂蚁到原点的距离相等时所对应的时间t.(写出解答过程)
(3)若小蚂蚁甲和乙约好分别从A,B两点,分别沿数轴甲向左,乙向右以相同的速度爬行,经过一段时间原路返回,刚好在16s时一起重新回到原出发点A和B,设小蚂蚁们出发t(s)时的速度为v(mm/s),v与t之间的关系如下图.(其中s表示时间单位秒,mm表示路程单位毫米)
t (s) | 0<t≤2 | 2<t≤5 | 5<t≤16 |
v(mm/s) | 10 | 16 | 8 |
①当2<t≤5时,你知道小蚂蚁甲与乙之间的距离吗?(用含有t的代数式表示);
②当t为__________________时,小蚂蚁甲乙之间的距离是42mm.(请直接写出答案)
![]()