题目内容
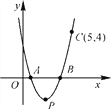
【题目】将一个正方形甲和两个正方形乙分别沿着图中虚线川剪刀剪成4个完全相等的长方形和一个正方形（如图1），已知正方形甲中剪出的小正方形面积是1，正方形乙中剪出的小正方形面积是4，现将剪得的12个长方形摆成如图2正方形
（不重叠无缝隙）．则正方形的面积是（）
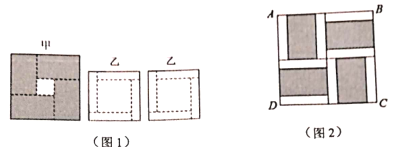
A.9B.16C.25D.36
【答案】C
【解析】
根据题意，设甲中分割出的长方形宽为x，则长为x+1，乙中分割出的长方形长为x+1，宽为x+1-2，由图（2）列出方程式2（x+1-2）+x=x+1，解得x值，求出乙图的正方形的边长即可得出面积．
根据题意，设甲中长方形分割的长方形的宽为x，则长为x+1，由图（2）可知，乙中分割出的长方形长为x+1，宽为x+1-2，则列出方程式可得
2（x+1-2）+x=x+1，
解得x=
，
图（2）中正方形的边长为2×（+1）=5，
所以正方形ABCD的面积为25，
故选：C．
练习册系列答案
相关题目
