题目内容
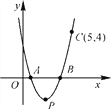
【题目】如图，抛物线y＝ax2－5ax＋4a与x轴相交于点A，B，且过点C(5，4)．
(1)求a的值和该抛物线顶点P的坐标；
(2)请你设计一种平移的方法，使平移后抛物线的顶点落在第二象限，并写出平移后抛物线的表达式．
【答案】(1) (
，－ 
)；(2)答案不唯一，合理即可，y＝x2＋x＋2.
【解析】试题分析：将点c坐标代入函数表达式即可求出a的值，a=1，将函数表达式转换为顶点式y＝x2－5x＋4＝(x－
)2－
，所以顶点坐标是（
，－ 
）；将抛物线平移后顶点在第二象限，答案不唯一，可通过平移顶点，例如先向左平移3个单位长度，则变为y＝ (x－
)2－
，再向上平移4个单位，得到y＝ (x－
)2－
+4= (x＋
)2＋
= x2＋x＋2.
解：(1)把点C(5，4)代入抛物线y＝ax2－5ax＋4a，得25a－25a＋4a＝4.解得a＝1.
∴二次函数的表达式为y＝x2－5x＋4.
∵y＝x2－5x＋4＝(x－
)2－
，
∴顶点P的坐标为(
，－ 
)．
(2)答案不唯一，合理即可，如：先向左平移3个单位长度，再向上平移4个单位长度，得到的二次函数表达式为y＝(x－
＋3)2－
＋4＝(x＋
)2＋
，
即y＝x2＋x＋2.
练习册系列答案
英才计划同步课时高效训练系列答案
相关题目
