题目内容
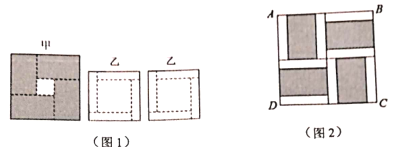
【题目】如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面,观察下列图形并解答有关问题:
 ……
……
n=1 n=2 n=3
(1)在第n个图中,共有 块白色瓷砖,共有 块黑色瓷砖(均用含n的代数式表示);
(2)设铺设地面所用瓷砖总数为y,请写出y与(1)中的n的函数关系式(不要求写出自变量的取值范围);
(3)若铺设这样的矩形地面共用了506块瓷砖,通过计算求此时n的值;
(4)是否存在n,使得黑瓷砖与白瓷砖块数相等?说明理由.
【答案】(1)n(n+1),4n+6;(2)y=n2+5n+6;(3)20;(4)不存在.
【解析】【试题分析】(1)第1个图形,白色瓷砖有![]() 个,黑色瓷砖有
个,黑色瓷砖有![]() 个;第2个图形中,白色瓷砖有
个;第2个图形中,白色瓷砖有![]() 个,黑色瓷砖有
个,黑色瓷砖有![]() 个;…则第n个图形中,白色瓷砖有
个;…则第n个图形中,白色瓷砖有![]() 个,黑色瓷砖有
个,黑色瓷砖有![]() 个;(2)根据(1)中分析,
个;(2)根据(1)中分析, ![]() ;
;
(3)由题意得: ![]() ,解得n1=20,n2=-25(不合题意,舍去).即n的值为20.
,解得n1=20,n2=-25(不合题意,舍去).即n的值为20.
(4)根据(1)中分析,得n(n+1)=4n+6.解得n1=![]() ,n2=
,n2=![]() ,(不是正整数,都舍去),则不存在n使得黑瓷砖与白瓷砖块数相等.
,(不是正整数,都舍去),则不存在n使得黑瓷砖与白瓷砖块数相等.
【试题解析】
(1)在第n个图中,共有n(n+1)块白色瓷砖,共有4n+6块黑色瓷砖;
(2)y=n2+5n+6.
(3)n2+5n+6=506.
解得n1=20,n2=-25(不合题意,舍去).
∴n的值为20.
(4)由题意,得n(n+1)=4n+6.
解得n1=![]() ,n2=
,n2=![]() (舍去).又因为
(舍去).又因为![]() 不是正整数,
不是正整数,
∴不存在n使得黑瓷砖与白瓷砖块数相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目