题目内容
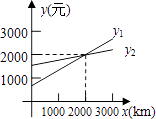
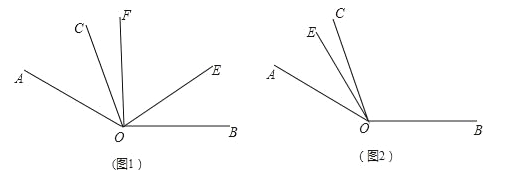
【题目】如图1,已知∠AOB=140°,∠AOC=30°,OE是∠AOB内部的一条射线,且OF平分∠AOE.
(1)若∠EOB=30°,则∠COF= ;
(2)若∠COF=20°,则∠EOB= ;
(3)若∠COF=n°,则∠EOB= (用含n的式子表示).
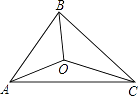
(4)当射线OE绕点O逆时针旋转到如图2的位置时,请把图补充完整;此时,∠COF与∠EOB有怎样的数量关系?请说明理由.
【答案】(1)25°;(2)40°;(3)80°﹣2n°;(4)∠EOB=80°+2∠COF.
【解析】试题分析:(1)先求出∠AOE,再根据角平分线的定义求出∠AOF,然后根据∠COF=∠AOF-∠AOC代入数据计算即可得解;
(2)先求出∠AOF,再根据角平分线的定义求出∠AOE,然后根据∠EOB=∠AOB-∠AOE代入数据计算即可得解;
(3)与(2)的思路相同求解即可;
(4)设∠COF=n°,先表示出∠AOF,然后根据角平分线的定义求出∠AOE,再根据∠EOB=∠AOB-∠AOE代入计算即可得解.
试题解析:
(1)∵∠AOB=140°,∠EOB=30°,
∴∠AOE=∠AOB-∠EOB=140°-30°=110°,
∵OF平分∠AOE,
∴∠AOF=![]() ∠AOE=
∠AOE=![]() ×110°=55°,
×110°=55°,
∴∠COF=∠AOF-∠AOC,
=55°-30°,
=25°;
故答案为:25°;
(2)∵∠AOC=30°,∠COF=20°,
∴∠AOF=∠AOC+∠COF=30°+20°=50°,
∵OF平分∠AOE,
∴∠AOE=2∠AOF=2×50°=100°,
∴∠EOB=∠AOB-∠AOE=140°-100°=40°;
故答案为:40°;
(3)∵∠AOC=30°,∠COF=n°,
∴∠AOF=∠AOC+∠COF=30°+n°,
∵OF平分∠AOE,
∴∠AOE=2∠AOF=2(30°+n°)=60°+2n°,
∴∠EOB=∠AOB-∠AOE=140°-(60°+2n°)=80°-2n°;
故答案为:80°-2n°;
(4)如图所示:∠EOB=80°+2∠COF.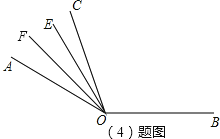
证明:设∠COF=n°,则∠AOF=∠AOC-∠COF=30°-n°,
又∵OF平分∠AOE,
∴∠AOE=2∠AOF=60°-2n°.
∴∠EOB=∠AOB-∠AOE=140°-(60°-2n°)=(80+2n)°
即∠EOB=80°+2∠COF.