Question

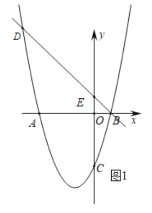
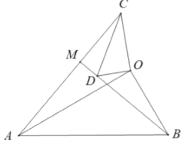
【题目】问题背景：如图 1，在和中，，连接 交的延长线于点．则的值是____________．

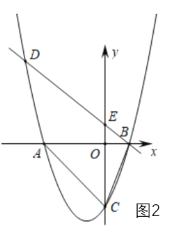
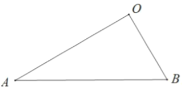
问题解决：如图 2，在问题背景的条件下，将绕点在平面内旋转，点始终在的外部，所在直线交于点，若，当点与点重合时，的长是____________

Answer 1

【答案】

【解析】

问题背景：根据两边的比相等且夹角相等可得△AOC∽△BOD，则；

问题解决：正确画图形，当点C与点M重合时，有两种情况：如图3和4，同理可得：△AOC∽△BOD，则∠AMB=90°，，可得AC的长．

解：问题背景：∵Rt△COD中，∠DCO=30°，∠DOC=90°，

∴，

同理得：，

∴，

∵∠AOB=∠COD=90°，
∴∠AOC=∠BOD，
∴△AOC∽△BOD，

∴；

问题解决：①点C与点M重合时，如图3，同理得：△AOC∽△BOD，
∴∠AMB=90°，，

设BD=x，则AC=x，

Rt△COD中，∠OCD=30°，OD=1，
∴CD=2，BC=x-2，
Rt△AOB中，∠OAB=30°，OB=，

∴AB=2OB=2，

在Rt△AMB中，由勾股定理得：AC2+BC2=AB2，

，

解得：x1=3，x2=-2，
∴AC=，

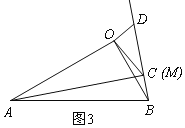
②点C与点M重合时，如图4，同理得：∠AMB=90°，，

设BD=x，则AC=x，

在Rt△AMB中，由勾股定理得：AC2+BC2=AB2，

，

解得：x1=-3，x2=2，
∴AC=2（不合题意舍去）；

综上所述，AC的长为3，

故答案为：；3.