题目内容
【题目】利用“同角的余角相等”可以帮助我们得到相等的角,这个规律在全等三角形的判定中有着广泛的运用.
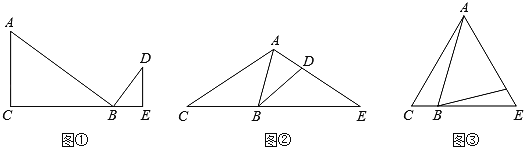
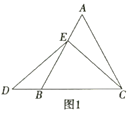
(1)如图①,![]() ,
,![]() ,
,![]() 三点共线,
三点共线,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() ,且
,且![]() .若
.若![]() ,求
,求![]() 的长.
的长.
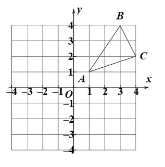
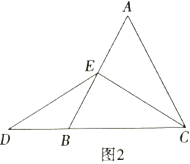
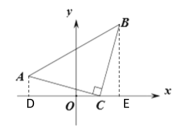
(2)如图②,在平面直角坐标系中,![]() 为等腰直角三角形,直角顶点
为等腰直角三角形,直角顶点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .求直线
.求直线![]() 与
与![]() 轴的交点坐标.
轴的交点坐标.
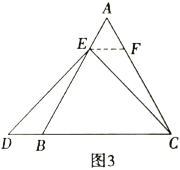
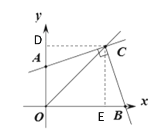
(3)如图③,![]() ,
,![]() 平分
平分![]() ,若点
,若点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() .则
.则![]() .(只需写出结果,用含
.(只需写出结果,用含![]() ,
,![]() 的式子表示)
的式子表示)

【答案】(1)6;(2)(0,2);(3)![]()
【解析】
(1)利用AAS证出△ABC≌△CDE,根据全等三角形的性质可得AB=CD,BC=DE,再根据BD=CD+BC等量代换即可求出BD;
(2)过点A作AD⊥x轴于D,过点B作BE⊥x轴于E,利用AAS证出△ADC≌△CEB,根据全等三角形的性质可得AD=CE,CD=BE,根据点A和点C的坐标即可求出点B的坐标,然后利用待定系数法求出直线AB的解析式,即可求出直线AB与y轴的交点坐标;
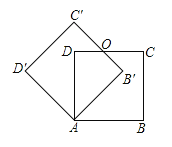
(3)过点C作CD⊥y轴于D,CE⊥x轴于E,根据正方形的判定可得四边形OECD是正方形,然后利用ASA证出△DCA≌△ECB,从而得出DA=EB,S△DCA=S△ECB,然后利用正方形的边长相等即可求出a、b表示出DA和正方形的边长OD,然后根据![]() 即可推出
即可推出![]() =
=![]() ,最后求正方形的面积即可.
,最后求正方形的面积即可.
解:(1)∵![]() ,
,![]() ,
,![]()
∴∠ABC=∠CDE=∠ACE=90°
∴∠A+∠ACB=90°,∠ECD+∠ACB=180°-∠ACE=90°
∴∠A=∠ECD
在△ABC和△CDE中
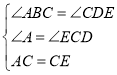
∴△ABC≌△CDE
∴AB=CD,BC=DE
∴BD=CD+BC=![]()
(2)过点A作AD⊥x轴于D,过点B作BE⊥x轴于E
∵△ABC为等腰直角三角形
∴∠ADC=∠CEB=∠ACB=90°,AC=CB
∴∠DAC+∠ACD=90°,∠ECB+∠ACD=180°-∠ACB=90°
∴∠DAC =∠ECB
在△ADC和△CEB中
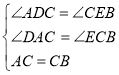
∴△ADC≌△CEB
∴AD=CE,CD=BE
∵点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
∴CO=1,AD=1,DO=2,
∴OE=OC+CE= OC+AD=2,BE=CD=CO+DO=3,
∴点B的坐标为(2,3)
设直线AB的解析式为y=kx+b
将A、B两点的坐标代入,得
![]()
解得:![]()
∴直线AB的解析式为![]()
当x=0时,解得y=2
∴直线![]() 与
与![]() 轴的交点坐标为(0,2);
轴的交点坐标为(0,2);
(3)过点C作CD⊥y轴于D,CE⊥x轴于E
∵OC平分∠AOB
∴CD=CE
∴四边形OECD是正方形
∴∠DCE=90°,OD=OE
∵∠ACB=90°
∴∠DCA+∠ACE=∠ECB+∠ACE=90°
∴∠DCA=∠ECB
在△DCA和△ECB中
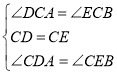
∴△DCA≌△ECB
∴DA=EB,S△DCA=S△ECB
∵点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]()
∴OB=b,OA=a
∵OD=OE
∴OA+DA=OB-BE
即a+DA=b-DA
∴DA=![]()
∴OD= OA+DA=![]()
![]()
=![]()
=![]()
= DA2
=![]()
=![]()
故答案为:![]() .
.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案