题目内容
【题目】在三角形纸片![]() 中,
中,![]() ,
,![]() ,点
,点![]() (不与
(不与![]() ,
,![]() 重合)是
重合)是![]() 上任意一点,将此三角形纸片按下列方式折叠,若
上任意一点,将此三角形纸片按下列方式折叠,若![]() 的长度为
的长度为![]() ,则
,则![]() 的周长为__________.(用含
的周长为__________.(用含![]() 的式子表示)
的式子表示)
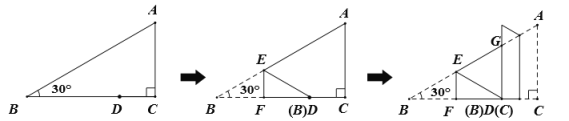
【答案】6![]()
【解析】
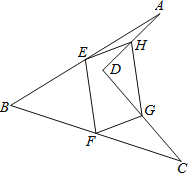
根据折叠的性质可得∠EDF=∠B=30°,∠EFB=∠EFD=90°,∠ACD=∠GDC=90°,然后根据三角形外角的性质和平角的定义即可求出∠GED、∠GDE,即可证出△EGD为等边三角形,从而得出EG=GD=ED,然后根据30°所对的直角边是斜边的一半即可求出ED,从而求出结论.
解:由折叠的性质可知:∠EDF=∠B=30°,∠EFB=∠EFD=90°,∠ACD=∠GDC=90°
∴∠GED=∠EDF+∠B=60°,∠GDE=180°-∠EDF-∠GDC=60°
∴∠EGD=180°-∠GED-∠GDE=60°
∴△EGD为等边三角形
∴EG=GD=ED
在Rt△EDF中,∠EDF=30°
∴ED=2EF=2![]()
∴EG=GD=ED=2![]()
∴![]() 的周长为EG+GD+ED=6
的周长为EG+GD+ED=6![]()
故答案为:6![]() .
.

练习册系列答案
相关题目